Lời giải chi tiết:

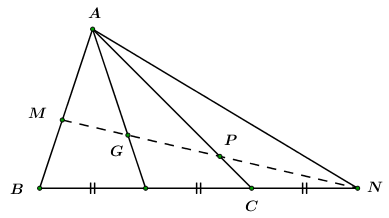
1.Ta có : \(3\overrightarrow {GA}  + 4\overrightarrow {GB}  = 7\overrightarrow {GM} \)

\(\begin{array}{l}\,\,\,\,\,\,\,\,\overrightarrow {GB}  - 3\overrightarrow {GC}  =  - 2\overrightarrow {GN} \\ \Rightarrow \overrightarrow {GB}  + 3\left( {\overrightarrow {GA}  + \overrightarrow {GB} } \right) =  - 2\overrightarrow {GN} \\ \Rightarrow 3\overrightarrow {GA}  + 4\overrightarrow {GB}  =  - 2\overrightarrow {GN} .\end{array}\)

Vậy : \(7\overrightarrow {GM}  =  - 2\overrightarrow {GN} \). Suy ra \(G,\,\,M,\,\,N\)  thẳng hàng.

2. Gọi \(E\)  là trung điểm của \(BC,\)  ta có :

\(\begin{array}{l}EC = EB = CN \Rightarrow 2\overrightarrow {AC}  = \overrightarrow {AE}  + \overrightarrow {AN} \\ \Rightarrow 2\overrightarrow {AC}  = \frac{3}{2}\overrightarrow {AG}  + \overrightarrow {AN}  \Rightarrow \overrightarrow {AC}  = \frac{3}{4}\overrightarrow {AG}  + \frac{1}{2}\overrightarrow {AN} .\end{array}\)

Gọi \(P'\)  là điểm thuộc đường thẳng \(GN\)  và thỏa mãn: \(\frac{3}{4}\overrightarrow {P'G}  + \frac{1}{2}\overrightarrow {P'N}  = \vec 0\)

Từ (*) ta có : \(\overrightarrow {AC}  = \left( {\frac{3}{4} + \frac{1}{2}} \right)\overrightarrow {AP'}  \Rightarrow A,\,\,C,\,\,P'\) thẳng hàng

Vậy : \(\left\{ {P'} \right\} = AC \cap GN \Rightarrow P' \equiv P \Rightarrow \overrightarrow {AC}  = \frac{5}{4}\overrightarrow {AP} .\)

\( \Rightarrow \overrightarrow {AP}  + \overrightarrow {PC}  = \frac{5}{4}\overrightarrow {AP}  \Rightarrow \overrightarrow {PC}  =  - \frac{1}{4}\overrightarrow {PA}  \Rightarrow \frac{{PA}}{{PC}} = 4.\)