Lời giải chi tiết:

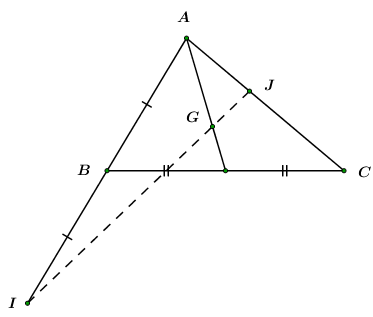
1. Ta có: \(\overrightarrow {IJ}  = \overrightarrow {AJ}  - \overrightarrow {AI} \).

+ Ta có \(\overrightarrow {IA}  = 2\overrightarrow {IB} \,\,\left( {gt} \right) \Rightarrow \overrightarrow {IA}  = 2\left( {\overrightarrow {IA}  + \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AI}  = 2\overrightarrow {AB} \)

+ Ta có: \(3\overrightarrow {JA}  + 2\overrightarrow {JC}  = \overrightarrow 0 \,\,\left( {gt} \right)\)

\( \Rightarrow 3\overrightarrow {JA}  + 2\left( {\overrightarrow {JA}  + \overrightarrow {AC} } \right) = \overrightarrow 0  \Leftrightarrow \overrightarrow {AJ}  = \frac{2}{5}\overrightarrow {AC} \)

+ Do đó: \(\overrightarrow {IJ}  = \overrightarrow {AJ}  - \overrightarrow {AI}  = \frac{2}{5}\overrightarrow {AC}  - 2\overrightarrow {AB} \).

2. Chứng minh \(I,\,\,\,G,\,\,J\)  thẳng hàng

Ta tính: \(\overrightarrow {IG} \)  theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).

Ta có: \(\overrightarrow {AG}  = \frac{1}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\) và \(\overrightarrow {AI}  = 2\overrightarrow {AB} \).

Suy ra: \(\overrightarrow {IG}  = \overrightarrow {AG}  - \overrightarrow {AI}  = \frac{1}{3}\overrightarrow {AB}  + \frac{1}{3}\overrightarrow {AC}  - 2\overrightarrow {AB}  = \frac{1}{3}\left( {\overrightarrow {AC}  - 5\overrightarrow {AB} } \right)\)

Ta có: \(\overrightarrow {IJ}  = \frac{2}{5}\left( {\overrightarrow {AC}  - 5\overrightarrow {AB} } \right) \Rightarrow \frac{{\overrightarrow {IG} }}{{\overrightarrow {IJ} }} = \frac{5}{6} \Rightarrow \overrightarrow {IG}  = \frac{5}{6}\overrightarrow {IJ} \).

Vậy 3 điểm \(I,\,\,\,G,\,\,J\) thẳng hàng.