Câu hỏi
Cho \(\Delta ABC,\) đặt \(\overrightarrow{AB}=\vec{u},\,\overrightarrow{AC}=\vec{v}.\)
1.Gọi \(P\) là điểm đối xứng của \(B\) qua \(C.\) Tính \(\overrightarrow{AP}\,\,\,theo~\,\,\vec{u},\,\,\,\vec{v}.\)
2. Gọi \(Q\) và \(R\) là \(2\) điểm định bởi: \(\overrightarrow{AQ}=\frac{1}{2}\overrightarrow{AC},\,\,\,\overrightarrow{AR}=\frac{1}{3}\overrightarrow{AB}.\) Tính \(\overrightarrow{RP},\,\,\,\,\overrightarrow{RQ}\,\,\,\,\,theo\,\,\,\,\vec{u},\,\,\,\vec{v}.\)
3. Suy ra \(3\) điểm \(P,\,\,Q,\,\,R\) thẳng hàng.
Lời giải chi tiết:
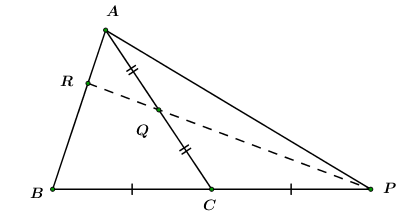
1. Xét \(\Delta APB,\) ta có: \(2\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AP} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {AP} = 2\overrightarrow {AC} - \overrightarrow {AB} \\ \Rightarrow \overrightarrow {AP} = 2\vec v - \vec u.\end{array}\)
\(\begin{array}{l}
2.\,\,\overrightarrow {RP} = \overrightarrow {RA} + \overrightarrow {AP} = - \frac{1}{3}\overrightarrow {AB} + \overrightarrow {AP} = - \frac{1}{3}\vec u + 2\vec v - \vec u = 2\vec v - \frac{4}{3}\vec u = \frac{4}{6}\left( {3\vec v - \overrightarrow {2u} } \right)\,\,\,\,\left( 1 \right)\\
\overrightarrow {RQ} = \overrightarrow {RA} + \overrightarrow {AQ} = - \frac{1}{3}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} = - \frac{1}{3}\vec u + \frac{1}{2}\vec v = \frac{1}{6}\left( {3\vec v - 2\vec u} \right)\,\,\,\left( 2 \right)
\end{array}\)
3.Từ (1) và (2) ta có : \(\overrightarrow {RP} = 4\overrightarrow {RQ} \)
Do đó \(\overrightarrow{RP},\,\,\overrightarrow{RQ}\) cùng phương, và có chung điểm gốc \(R\) nên \(P,\,\,Q,\,\,R\) thẳng hàng.







