Phương pháp giải:

Cách 1: Tính y’, giải phương trình \(y' = 0\)

Lập BBT rồi suy ra các điểm cực trị của hàm số.

Điểm \({x_0}\) được gọi là điểm cực đại (cực tiểu) của đồ thị hàm số khi và chỉ khi y’ đổi dấu từ dương (âm) sang âm (dương).

Cách 2: Điểm \({x_0}\) được gọi là điểm cực đại (cực tiểu) của đồ thị hàm số \( \Leftrightarrow \left\{ \matrix{  f'\left( {{x_0}} \right) = 0 \hfill \cr   f''\left( {{x_0}} \right) < 0 \hfill \cr}  \right.\,\,\,\left( {\left\{ \matrix{  f'\left( {{x_0}} \right) = 0 \hfill \cr   f''\left( {{x_0}} \right) > 0 \hfill \cr}  \right.} \right)\)

Lời giải chi tiết:

Cách 1:

TXĐ : D = R.

Ta có: \(y' = 3{x^2} - 3,\,\,y' = 0 \Leftrightarrow 3{x^2} - 3 = 0 \Leftrightarrow \left[ \matrix{  x = 1 \Rightarrow y = 0 \hfill \cr   x =  - 4 \Rightarrow y = 0 \hfill \cr}  \right.\)

BBT:

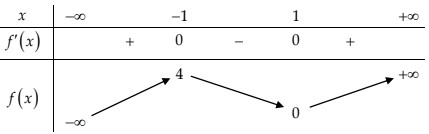
Từ BBT ta thấy \({x_0} =  - 1\) là điểm cực đại của hàm số.

Cách 2:

TXĐ : D = R.

Ta có: \(y' = 3{x^2} - 3;\,\,y'' = 6x\)

Xét hệ phương trình \(\left\{ \matrix{  y' = 0 \hfill \cr   y'' < 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  3{x^2} - 3 = 0 \hfill \cr   6x < 0 \hfill \cr}  \right. \Leftrightarrow \left[ \matrix{  x =  \pm 1 \hfill \cr   x < 0 \hfill \cr}  \right. \Leftrightarrow x =  - 1.\)

Vậy \({x_0} =  - 1\) là điểm cực đại của hàm số.

Chọn B.