Câu hỏi
Cho hàm số \(f\left( x \right)=\left( {{m}^{2018}}+1 \right){{x}^{4}}+\left( -\,2{{m}^{2018}}-{{2}^{2018}}{{m}^{2}}-3 \right){{x}^{2}}+{{m}^{2018}}+2018,\) với \(m\) là tham số. Số cực trị của hàm số \(y=\left| f\left( x \right)-2017 \right|\) là
- A 7
- B 5
- C 3
- D 6
Phương pháp giải:
Chuẩn hóa tham số và dựa vào cách vẽ đồ thị hàm số \(y=\left| f\left( x \right) \right|\) để xác định điểm cực trị và giá trị cực trị của hàm số
Lời giải chi tiết:
Chọn \(m=0,\) khi đó
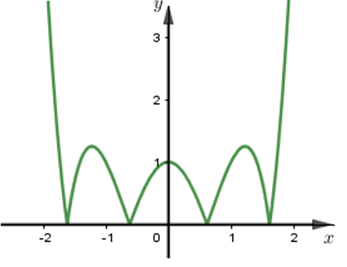
\(f\left( x \right)={{x}^{4}}-3{{x}^{2}}+2018\)\(\Rightarrow g\left( x \right)=\left| f\left( x \right)-2017 \right|=\left| {{x}^{4}}-3{{x}^{2}}+1 \right|\)
Dựa vào đồ thị hàm số \(g\left( x \right)=\left| {{x}^{4}}-3{{x}^{2}}+1 \right|\Rightarrow \) Hàm số \(y=\left| f\left( x \right)-2017 \right|\) có 7 cực trị.
Chọn A.
Câu hỏi trước
