Câu hỏi
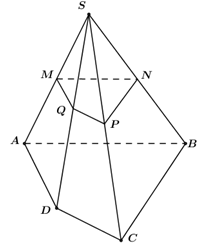
Cho hình chóp \(S.ABCD.\) Gọi \(M,\,\,N,\,\,P,\,\,Q\) theo thứ tự là trung điểm của \(SA,\,\,SB,\,\,SC,\,\,SD.\) Tỉ số thể tích của hai khối chóp \(S.MNPQ\) và \(S.ABCD\) bằng
- A \(\frac{1}{8}.\)
- B \(\frac{1}{2}.\)
- C \(\frac{1}{4}.\)
- D \(\frac{1}{16}.\)
Phương pháp giải:
Sử dụng công thức tỉ số thể tích (Định lí Simpson) : \(\frac{{{V}_{SABC}}}{{{V}_{SA'B'C'}}}=\frac{SA}{SA'}.\frac{SB}{SB'}.\frac{SC}{SC'}\) với \(A'\in SA;\ B'\in SB;\ C'\in SC\).
Lời giải chi tiết:
Ta có \(\frac{{{V}_{S.MNP}}}{{{V}_{S.ABC}}}=\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SC}=\frac{1}{8};\) \(\frac{{{V}_{S.MQP}}}{{{V}_{S.ADC}}}=\frac{SM}{SA}.\frac{SQ}{SD}.\frac{SP}{SC}=\frac{1}{8}.\)
Khi đó \(\frac{{{V}_{S.MNP}}+{{V}_{S.MQP}}}{\frac{1}{2}{{V}_{S.ABCD}}}=\frac{1}{8}+\frac{1}{8}\Leftrightarrow \frac{{{V}_{S.MNPQ}}}{{{V}_{S.ABCD}}}=\frac{2}{8}.\frac{1}{2}=\frac{1}{8}.\)
Chọn A