Câu hỏi
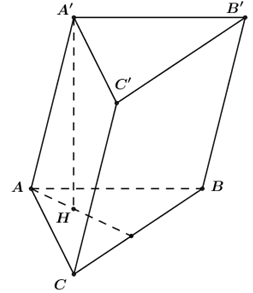
Cho khối lăng trụ \(ABC.{A}'{B}'{C}'\) có đáy \(ABC\) là tam giác đều cạnh bằng \(a,\) cạnh bên \(A{A}'=a,\) góc giữa đường thẳng \(A{A}'\) và mặt phẳng đáy bằng \({{30}^{0}}.\) Tính thể tích khối lăng trụ đã cho theo \(a.\)
- A \(\frac{{{a}^{3}}\sqrt{3}}{24}.\)
- B \(\frac{{{a}^{3}}\sqrt{3}}{12}.\)
- C \(\frac{{{a}^{3}}\sqrt{3}}{4}.\)
- D \(\frac{{{a}^{3}}\sqrt{3}}{8}.\)
Phương pháp giải:
Gọi hình chiếu của đỉnh, xác định góc từ đó tính chiều cao suy ra thể tích khối lăng trụ.
Công thức tính thể tích lăng trụ : \(V={{S}_{d}}.h.\)
Lời giải chi tiết:
Gọi \(H\) là hình chiếu của \({A}'\) trên mặt phẳng \(\left( ABC \right)\)\(\Rightarrow \,\,{A}'H\bot \left( ABC \right).\)
Suy ra \(\widehat{A{A}';\left( ABC \right)}=\widehat{\left( A{A}';AH \right)}=\widehat{{A}'AH}={{30}^{0}}.\)
Tam giác \({A}'AH\) vuông tại \(H,\) có \(\sin \widehat{{A}'AH}=\frac{{A}'H}{A{A}'}\Rightarrow {A}'H=\frac{a}{2}.\)
Diện tích tam giác \(ABC\) là \({{S}_{\Delta \,ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}.\)
Vậy thể tích khối lăng trụ đã cho là \(V={A}'H.{{S}_{\Delta \,ABC}}=\frac{a}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{8}.\)
Chọn D