Câu hỏi
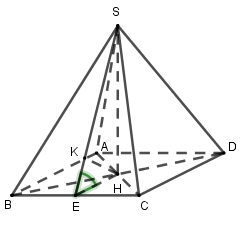
Cho hình chóp tứ giác đều có mặt bên hợp với đáy một góc 450 và khoảng cách từ chân đường cao đến mặt bên bằng \(a\). Tính thể tích của khối chóp đó.
- A \(V = \frac{{{a^3}\sqrt 3 }}{9}\)
- B \(V = \frac{{8{a^3}\sqrt 2 }}{3}\)
- C \(V = \frac{{{a^3}\sqrt 3 }}{6}\)
- D \(V = \frac{{{a^3}\sqrt 3 }}{4}\)
Phương pháp giải:
+) Xác định góc giữa mặt bên và đáy.
+) Xác định khoảng cách từ chân đường cao đến mặt bên.
+) Áp dụng công thức tính thể tích \({V_{S.ABCD}} = \frac{1}{3}h.{S_d}\)
Lời giải chi tiết:
Gọi \(H\) là tâm tam hình vuông \(ABCD \Rightarrow SH \bot \left( {ABCD} \right)\)
Gọi \(E\) là trung điểm của \(BC\) ta có : \(\left\{ \begin{array}{l}BC \bot AE\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\)
\( \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SE;AE} \right)} = \widehat {SEA} = {45^0}\)
Trong \(\left( {SAE} \right)\) kẻ \(HK \bot SE \Rightarrow HK \bot \left( {SBC} \right) \Rightarrow HK = a\)
\(\begin{array}{l} \Rightarrow HE = \frac{{HK}}{{\cos 45}} = a\sqrt 2 \\\Rightarrow AB = 2HE = 2a\sqrt 2 \Rightarrow {S_{ABCD}} = 8{a^2}\\SH = HE.\tan 45 = a\sqrt 2 \\\Rightarrow {V_{S.ABCD}} = \frac{1}{3}.a\sqrt 2 .8{a^2} = \frac{{8{a^3}\sqrt 2 }}{3}\end{array}\)
Chọn B.