Phương pháp giải:

Xác định thể tích khối chóp thông qua phương pháp dựng hình với các yếu tố đặc biệt, đưa về biểu thức chứa hai biến \(x,\,\,y\) và đánh giá thông qua bất đẳng thức, khảo sát hàm số để tìm GTLN của thể tích

Lời giải chi tiết:

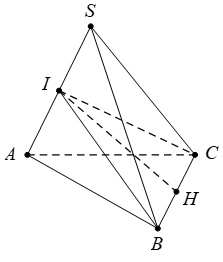
Gọi \(I,\,\,H\) lần lượt là trung điểm của \(SA,\,\,BC.\) Ta có \(\left\{ \begin{align}  & BI\bot SA \\ & CI\bot SA \\\end{align} \right.\Rightarrow SA\bot \left( BIC \right)\) và \({{V}_{S.IBC}}={{V}_{A.IBC}}.\)

Lại có \(BI=\sqrt{S{{B}^{2}}-S{{I}^{2}}}=\sqrt{1-\frac{{{x}^{2}}}{4}}=\frac{\sqrt{4-{{x}^{2}}}}{2}.\)

Và \(IH=\sqrt{I{{B}^{2}}-B{{H}^{2}}}=\sqrt{\frac{4-{{x}^{2}}}{4}-\frac{{{y}^{2}}}{4}}=\frac{\sqrt{4-{{x}^{2}}-{{y}^{2}}}}{2}.\)

Diện tích tam giác \(IBC\) là \({{S}_{\Delta \,IBC}}=\frac{1}{2}.IH.BC=\frac{y}{4}\sqrt{4-{{x}^{2}}-{{y}^{2}}}.\)

Suy ra \({{V}_{S.IBC}}={{V}_{A.IBC}}=\frac{1}{3}.\frac{x}{2}.\frac{y}{4}\sqrt{4-{{x}^{2}}-{{y}^{2}}}=\frac{xy}{24}\sqrt{4-{{x}^{2}}-{{y}^{2}}}.\)

Khi đó, thể tích khối chóp \(S.ABC\) là \({{V}_{S.ABC}}=2\,{{V}_{S.IBC}}=\frac{xy}{12}\sqrt{4-{{x}^{2}}-{{y}^{2}}}.\)

Ta có \(xy\le \frac{{{x}^{2}}+{{y}^{2}}}{2}\)\(\Rightarrow \)\(V\le \frac{{{x}^{2}}+{{y}^{2}}}{24}\sqrt{4-{{x}^{2}}-{{y}^{2}}}.\)

Đặt \(t=\sqrt{4-{{x}^{2}}-{{y}^{2}}}\in \left( 0;2 \right),\) khi đó \(V\le f\left( t \right)=\frac{t\left( 4-{{t}^{2}} \right)}{24}\le \frac{16\sqrt{3}}{9}\) (khảo sát hàm số).

Vậy giá trị lớn nhất của \({{V}_{S.ABC}}\) là \({{V}_{\max }}=\frac{2\sqrt{3}}{27}.\)

Chọn B.