Phương pháp giải:

Đồ thị hàm số \(y = \left| {a{x^4} + b{x^2}} \right|\,\,\,\left( {a \ne 0} \right)\) được xác định bằng cách: Từ đồ thị hàm số \(y = a{x^4} + b{x^2}\,\,\,\left( {a \ne 0} \right)\), lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành, sau đó bỏ đi phần đồ thị phía dưới trục hoành.

Lời giải chi tiết:

Xét đồ thị hàm số \(y = a{x^4} + b{x^2}\,\,\,\left( {a \ne 0} \right)\)có \(y' = 4a{x^3} + 2bx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0\\x =  - \frac{b}{{2a}}\end{array} \right.\) có nhiều nhất 3 điểm cực trị khi \( - \frac{b}{{2a}} > 0 \Leftrightarrow ab < 0\), khi đó đồ thị hàm số có 1 điểm cực đại \(\left( {0;0} \right)\) và 2 điểm cực tiểu.

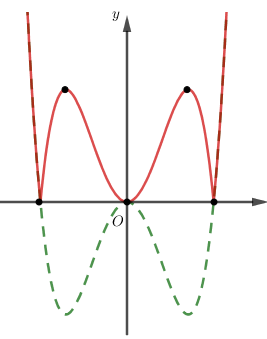
Đồ thị hàm số \(y = \left| {a{x^4} + b{x^2}} \right|\,\,\,\left( {a \ne 0} \right)\) được xác định bằng cách: Từ đồ thị hàm số \(y = a{x^4} + b{x^2}\,\,\,\left( {a \ne 0} \right)\), lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành, sau đó bỏ đi phần đồ thị phía dưới trục hoành, khi đó đồ thị hàm số \(y = \left| {a{x^4} + b{x^2}} \right|\,\,\,\left( {a \ne 0} \right)\) có dạng như hình vẽ bên.

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có nhiều nhất 5 điểm cực trị.

Chọn D.