Câu hỏi
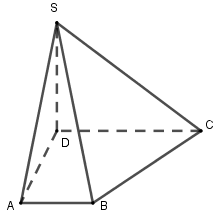
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), cạnh bên \(SD\) vuông góc với đáy. Biết \(AB = AD = a,CD = 3a,SA = a\sqrt 3 \). Tính thể tích khối chóp \(S.ABCD\).
- A \(\frac{{2{a^3}\sqrt 2 }}{3}\)
- B \(2{a^3}\sqrt 2 \)
- C \(\frac{{2{a^3}\sqrt 3 }}{3}\)
- D \(\frac{{{a^3}\sqrt 2 }}{3}\)
Phương pháp giải:
\({V_{S.ABCD}} = \frac{1}{3}SD.{S_{ABCD}}\)
Lời giải chi tiết:
\({S_{ABCD}} = \frac{1}{2}AD\left( {AB + CD} \right) = \frac{1}{2}.a.\left( {a + 3a} \right) = 2{a^2}\)
\(SD \bot \left( {ABCD} \right) \Rightarrow SD \bot AD \Rightarrow \Delta SACD\) vuông tại \(D\)
\( \Rightarrow SD = \sqrt {S{A^2} - A{D^2}} = a\sqrt 2 \)
\( \Rightarrow {V_{S.ABCD}} = \frac{1}{3}SD.{S_{ABCD}} = \frac{1}{3}a\sqrt 2 .2{a^2} = \frac{{2\sqrt 2 {a^3}}}{3}\)
Chọn A.
Câu hỏi trước
