Câu hỏi
Một hình trụ có diện tích xung quanh bằng \(4\pi ,\) thiết diện qua trục là hình vuông. Một mặt phẳng \(\left( \alpha \right)\) song song với trục, cắt hình trụ theo thiết diện là tứ giác \(AB{B}'{A}',\) biết một cạnh của thiết diện là một dây cung của đường tròn đáy của hình trụ và căng một cung \({{120}^{0}}.\) Tính diện tích thiết diện \(AB{B}'{A}'.\)
- A \(3\sqrt{2}.\)
- B \(\sqrt{3}.\)
- C \(2\sqrt{3}.\)
- D \(2\sqrt{2}.\)
Phương pháp giải:
Mặt phẳng song song với trục cắt hình trụ theo thiết diện là một hình chữ nhật.
Vẽ hình, xác định độ dài đường sinh và bán kính đáy để tính diện tích tứ giác
Lời giải chi tiết:
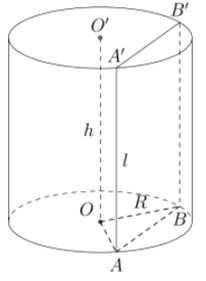
Gọi \(R,\,\,h,\,\,l\) lần lượt là bán kính đáy, chiều cao, đường sinh của hình trụ.
Ta có diện tích xung quanh \({{S}_{xq}}=4\pi \Leftrightarrow 2\pi Rl=4\pi \Rightarrow Rl=2.\)
Giả sử \(AB\) là một dây cung của đường tròn đáy của hình trụ và căng một cung \({{120}^{0}}.\) Vì \(AB{B}'{A}'\) là hình chữ nhật có \(A{A}'=h=l.\)
Xét tam giác \(OAB\) cân tại \(O,\) có \(\left\{ \begin{align} & OA=OB=R \\ & \widehat{AOB}={{120}^{0}} \\\end{align} \right.\Rightarrow AB=R\sqrt{3}.\)
Vậy diện tích cần tính là \({{S}_{AB{B}'{A}'}}=AB.A{A}'=R\sqrt{3}.l=2\sqrt{3}.\)
Chọn C.