Câu hỏi
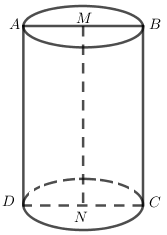
Cho hình chữ nhật \(ABCD\) cạnh \(AB = 4,AD = 6\). Gọi \(M,N\) là trung điểm các cạnh \(AB\) và \(CD\). Cho hình chữ nhật \(ABCD\) quay qanh \(MN\) ta được hình trụ tròn xoay có thể tích bằng:
- A \(V = 96\pi \)
- B \(V = 12\pi \)
- C \(V = 36\pi \)
- D \(V = 24\pi \)
Phương pháp giải:
Thể tích khối trụ \(V = \pi {R^2}h\)
Lời giải chi tiết:
Quay hình chữ nhật \(ABCD\) quanh \(MN\) ta được hình trụ có đường cao \(AD = 6\) và bán kính đáy bằng \(\frac{{AB}}{2} = 2\)
Vậy thể tích của khối trụ \(V = \pi {.2^2}.6 = 24\pi \)
Chọn D.
Câu hỏi trước
