Phương pháp giải:

Giải phương trình đạo hàm bằng 0, xác định điểm cực trị và lập bảng biến thiên, đánh giá khoảng đồng biến và nghịch biến của hàm số.

Lời giải chi tiết:

Ta có \({f}'\left( x \right)={{\left( x+1 \right)}^{2}}\left( x-1 \right)\left( 5-x \right)\,\,\xrightarrow{{}}\,\,{f}'\left( x \right)=0\Leftrightarrow \left[ \begin{align}  & x=\pm \,1 \\  & x=5 \\ \end{align} \right..\)

Bảng biến thiên

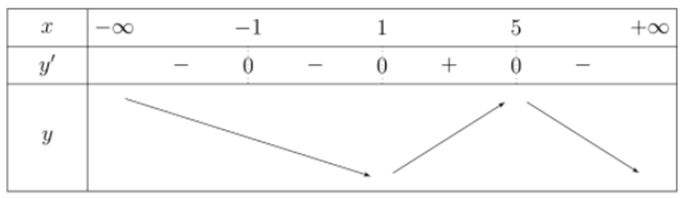
Suy ra hàm số đồng biến trên khoảng \(\left( 1;5 \right)\)\(\Rightarrow f\left( 1 \right)<f\left( 2 \right)<f\left( 4 \right).\)

Chọn B.