Câu hỏi
Cho \(\Delta ABC,\) gọi \({A_1},\,\,{B_1},\,\,{C_1}\) lần lượt là trung điểm của \(BC,\,\,CA,\,\,AB.\)
1.Chứng minh rằng \(\overrightarrow {A{A_1}} + \overrightarrow {B{B_1}} + \overrightarrow {C{C_1}} = \overrightarrow 0 .\)
2.Đặt \(\overrightarrow {B{B_1}} = \overrightarrow u ,\,\,\,\overrightarrow {C{C_1}} = \overrightarrow v .\) Tính \(\overrightarrow {BC} ,\,\,\overrightarrow {CA} ,\,\,\overrightarrow {AB} \) theo \(\overrightarrow u ,\,\,\overrightarrow v .\)
- A \(\begin{array}{*{20}{l}}
{\overrightarrow {BC} = \frac{2}{3}\vec u - \frac{2}{3}\vec v}\\
{\overrightarrow {AB} = - \frac{4}{3}\vec u - \frac{2}{3}\vec v}\\
{\overrightarrow {CA} = \frac{2}{3}\vec u + \frac{4}{3}\vec v}
\end{array}\) - B \(\begin{array}{*{20}{l}}
{\overrightarrow {BC} = \frac{2}{3}\vec u - \frac{2}{3}\vec v}\\
{\overrightarrow {AB} = \frac{4}{3}\vec u + \frac{2}{3}\vec v}\\
{\overrightarrow {CA} = \frac{2}{3}\vec u + \frac{4}{3}\vec v}
\end{array}\) - C \(\begin{array}{l}
\overrightarrow {BC} = \frac{2}{3}\overrightarrow u + \frac{2}{3}\overrightarrow v \\
\overrightarrow {AB} = \frac{4}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v \\
\overrightarrow {CA} = \frac{2}{3}\overrightarrow u - \frac{4}{3}\overrightarrow v
\end{array}\) - D \(\begin{array}{l}
\overrightarrow {BC} = - \frac{2}{3}\overrightarrow u - \frac{2}{3}\overrightarrow v \\
\overrightarrow {AB} = \frac{4}{3}\overrightarrow u + \frac{2}{3}\overrightarrow v \\
\overrightarrow {CA} = 2\overrightarrow u + \frac{4}{3}\overrightarrow v
\end{array}\)
Lời giải chi tiết:
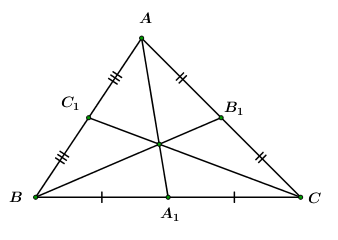
1. Theo quy tắc hình bình hành ta có: \(\left\{ \begin{array}{l}2\overrightarrow {A{A_1}} = \overrightarrow {AB} + \overrightarrow {AC} \\2\overrightarrow {B{B_1}} = \overrightarrow {BA} + \overrightarrow {BC} \\2\overrightarrow {C{C_1}} = \overrightarrow {CA} + \overrightarrow {CB} \end{array} \right..\)
\(\begin{array}{l} \Rightarrow 2\left( {\overrightarrow {A{A_1}} + \overrightarrow {B{B_1}} + \overrightarrow {C{C_1}} } \right) = \left( {\overrightarrow {AB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {AC} + \overrightarrow {CA} } \right) + \left( {\overrightarrow {BC} + \overrightarrow {CB} } \right) = \overrightarrow 0 \\ \Rightarrow \overrightarrow {A{A_1}} + \overrightarrow {B{B_1}} + \overrightarrow {C{C_1}} = \overrightarrow 0 .\end{array}\)
2. Ta có: \(\left\{ \begin{array}{l}\overrightarrow {BA} + \overrightarrow {BC} = 2\overrightarrow {B{B_1}} = 2\overrightarrow u \\\overrightarrow {CA} + \overrightarrow {CB} = 2\overrightarrow {C{C_1}} = 2\overrightarrow v \end{array} \right.\)
\( \Rightarrow \left( {\overrightarrow {CB} + \overrightarrow {BA} } \right) + \overrightarrow {CB} = 2\overrightarrow {CB} + \overrightarrow {BA} = 2\overrightarrow v .\)
Vậy: \(\left\{ \begin{array}{l}2\overrightarrow u = \overrightarrow {BA} + \overrightarrow {BC} \\2\overrightarrow v = \overrightarrow {BA} - 2\overrightarrow {BC} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {BC} = \frac{2}{3}\left( {\overrightarrow u - \overrightarrow v } \right)\\\overrightarrow {BA} = \frac{2}{3}\left( {2\overrightarrow u + \overrightarrow v } \right)\end{array} \right. \Rightarrow \overrightarrow {CA} = \overrightarrow {CB} + \overrightarrow {BA} = \frac{2}{3}\left( {2\overrightarrow v + \overrightarrow u } \right).\)







