Câu hỏi
Cho \(\Delta ABC,\) bên ngoài \(\Delta ABC,\) ta vẽ hình bình hành \(ABIJ,\,\,\,BCPQ,\,\,CARS.\) Chứng minh rằng:\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 .\)
Lời giải chi tiết:
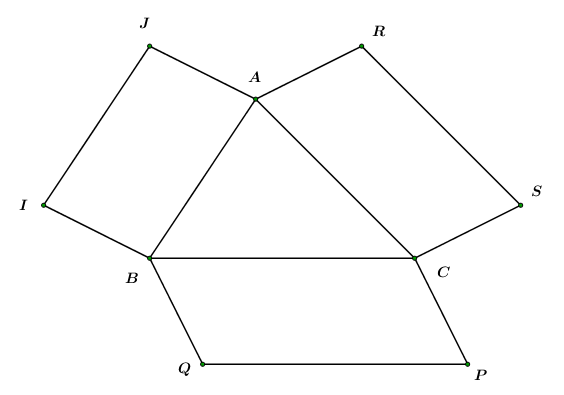
Ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\overrightarrow {RJ} + \overrightarrow {JI} + \overrightarrow {IQ} + \overrightarrow {QP} + \overrightarrow {PS} + \overrightarrow {SR} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {RJ} + \overrightarrow {AB} + \overrightarrow {IQ} + \overrightarrow {BC} + \overrightarrow {PS} + \overrightarrow {CA} = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} + \left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 .\end{array}\)







