Phương pháp giải:

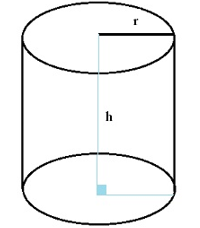
+) Diện tích xung quanh hình trụ tròn xoay bằng tích của độ dài đường tròn đáy và độ dài đường sinh:

\({{S}_{xq}}=2\pi Rl=2\pi Rh\)

+) Diện tích toàn phần hình trụ tròn xoay bằng tổng diện tích xung quanh và diện tích 2 đáy:

\({{S}_{tp}}={{S}_{xq}}+{{S}_{2\,\,day}}=2\pi Rl+2\pi {{R}^{2}}=2\pi Rh+2\pi {{R}^{2}}\)

Lời giải chi tiết:

\({{S}_{tp}}=2\pi Rh+2\pi {{R}^{2}}=2\pi .a.a\sqrt{3}+2\pi {{a}^{2}}=2\sqrt{3}\pi {{a}^{2}}+2\pi {{a}^{2}}=2\pi {{a}^{2}}\left( \sqrt{3}+1 \right)\)

Chọn: B