Câu hỏi
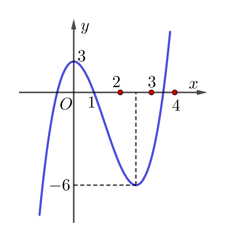
Cho hàm số \(y=f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị là đường cong trong hình vẽ bên. Đặt \(g\left( x \right)=f\left[ f\left( x \right) \right].\) Tìm số nghiệm của phương trình \({g}'\left( x \right)=0.\)
- A 2
- B 8
- C 4
- D 6
Phương pháp giải:
Áp dụng bài toán đọc đồ thị để xác định số nghiệm của phương trình.
Lời giải chi tiết:
Ta có \(g'\left( x \right)=\left[ f\left[ f\left( x \right) \right] \right]'=f'\left[ f\left( x \right) \right].f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} f'\left[ f\left( x \right) \right]=0 \\ f'\left( x \right)=0 \\ \end{align} \right.\)
Do đồ thị hàm số \(y=f\left( x \right)\) có 2 điểm cực trị nên \(f'\left( x \right)=0\) có 2 nghiệm.
Lại có \(f'\left[ f\left( x \right) \right]=0\Leftrightarrow \left[ \begin{align} f\left( x \right)=0 \\ f\left( x \right)\approx \frac{5}{2} \\ \end{align} \right.\); trong đó \(f\left( x \right)=0\) có 3 nghiệm; \(f\left( x \right)\approx 2,5\) có 3 nghiệm.
Vậy PT \(g'\left( x \right)=0\) có 8 nghiệm phân biệt.
Chọn B







