Phương pháp giải:

Sử dụng phương pháp xác định góc giữa hai mặt phẳng, tìm các yếu tố liên quan đến chiều cao của khối chóp suy ra thể tích khối chóp

Lời giải chi tiết:

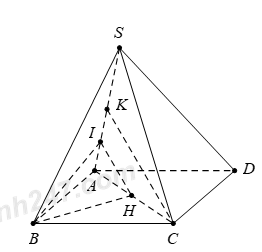
Kẻ \(BH\bot AC\,\,\,\left( H\in AC \right),\,\,\,HI\bot SA\,\,\,\left( I\in SA \right)\)

Suy ra \(\widehat{\left( \left( SAB \right);\left( SAC \right) \right)}=\widehat{\left( BI;HI \right)}=\widehat{BIH}\Rightarrow \tan \widehat{BIH}=\frac{3}{2}.\)

Tam giác \(BIH\) vuông tại \(H,\) có \(\tan \widehat{BIH}=\frac{BH}{IH}\Rightarrow IH=\frac{2\sqrt{2}}{3}.\)

Gọi \(K\) là trung điểm của \(SA,\,\,\Delta \,SAC\) cân tại \(C\Rightarrow CK\bot SA.\)

Suy ra \(IH\)//\(CK\)\(\Rightarrow \,\,\frac{AH}{AC}=\frac{IH}{CK}=\frac{1}{3}\Rightarrow CK=3\,IH=3.\frac{2\sqrt{2}}{3}=2\sqrt{2}.\)

Mặt khác \({{S}_{\Delta \,SAC}}=\frac{1}{2}.CK.SA=\frac{1}{2}d\left( S;\left( AC \right) \right).AC\Rightarrow d\left( S;\left( AC \right) \right)=\frac{2\sqrt{2}.2}{3}=\frac{4\sqrt{2}}{3}.\)

Vậy thể tích cần tính là \({{V}_{S.ABCD}}=\frac{1}{3}.d\left( S;\left( AC \right) \right).{{S}_{ABCD}}=\frac{1}{3}.\frac{4\sqrt{2}}{3}.3\sqrt{2}=\frac{8}{3}.\)

Chọn A