Phương pháp giải:

Điểm x₀ được gọi là điểm cực trị của hàm số \(y=f\left( x \right)\) nếu f(x) xác định tại x₀ và qua x₀ đồ thị hàm số đổi chiều.

Lời giải chi tiết:

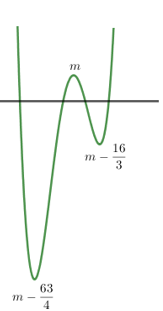
Xét hàm số \(y=\frac{{{x}^{4}}}{4}+\frac{{{x}^{3}}}{3}-3{{x}^{2}}+m\) có \(y'={{x}^{3}}+{{x}^{2}}-6x=0\Leftrightarrow \left[ \begin{align}  x=0 \\   x=2 \\   x=-3 \\ \end{align} \right.\)

Đồ thị hàm số có dạng  như hình vẽ bên:

Đồ thị hàm số \(f\left( x \right)=\left| \frac{{{x}^{4}}}{4}+\frac{{{x}^{3}}}{3}-3{{x}^{2}}+m \right|\) được vẽ bằng cách lấy đối

xứng phần đồ thị phía dưới trục Ox của hàm số \(y=\frac{{{x}^{4}}}{4}+\frac{{{x}^{3}}}{3}-3{{x}^{2}}+m\) qua trục

Ox sau đó bỏ đi phần đồ thị hàm số phía dưới trục Ox.

Do đó để đồ thị hàm số \(f\left( x \right)=\left| \frac{{{x}^{4}}}{4}+\frac{{{x}^{3}}}{3}-3{{x}^{2}}+m \right|\) có 7 cực trị thì \(m-\frac{16}{3}<0<m\Leftrightarrow 0<m<\frac{16}{3}\). Mà \(m\in Z\Rightarrow m\in \left\{ 1;2;3;4; 5 \right\}\) .

Chọn C.