Câu hỏi
Cho hàm số \(y={{x}^{3}}-\frac{3}{4}{{x}^{2}}-\frac{3}{2}x\) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của m sao cho phương trình \(4\left| {{x}^{3}} \right|-3{{x}^{2}}-6\left| x \right|={{m}^{2}}-6m\) có đúng ba nghiệm phân biệt.
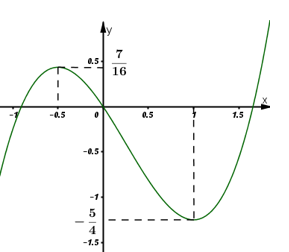
- A \(0<m<3\)
- B \(m=0\) hoặc \(m=6\)
- C \(m>0\) hoặc \(m<6\)
- D \(1<m<6\)
Phương pháp giải:
\(4\left| {{x}^{3}} \right|-3{{x}^{2}}-6\left| x \right|={{m}^{2}}-6m\Leftrightarrow \left| {{x}^{3}} \right|-\frac{3}{4}\left| {{x}^{2}} \right|-\frac{3}{2}\left| x \right|=\frac{{{m}^{2}}}{4}-\frac{3}{2}m\Rightarrow \)Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y=\left| f\left( x \right) \right|\) và đường thẳng \(y=\frac{{{m}^{2}}}{4}-\frac{3}{2}m\) song song với trục hoành.
Lời giải chi tiết:
\(4\left| {{x}^{3}} \right|-3{{x}^{2}}-6\left| x \right|={{m}^{2}}-6m\Leftrightarrow \left| {{x}^{3}} \right|-\frac{3}{4}\left| {{x}^{2}} \right|-\frac{3}{2}\left| x \right|=\frac{{{m}^{2}}}{4}-\frac{3}{2}m\Rightarrow f\left( \left| x \right| \right)=\frac{{{m}^{2}}}{4}-\frac{3}{2}m\Rightarrow \) Số nghiệm của phương trình là số giao điểm của đồ thị hàm số \(y=\left| f\left( x \right) \right|\) và đường thẳng \(y=\frac{{{m}^{2}}}{4}-\frac{3}{2}m\) song song với trục hoành.
Từ đồ thị hàm số \(y={{x}^{3}}-\frac{3}{4}{{x}^{2}}-\frac{3}{2}x\) ta suy ra đồ thị hàm số \(y=\left| {{x}^{3}} \right|-\frac{3}{4}\left| {{x}^{2}} \right|-\frac{3}{2}\left| x \right|\) như sau:

Để phương trình có đúng 3 nghiệm phân biệt thì \(\frac{{{m^2}}}{4} - \frac{3}{2}m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 6\end{array} \right.\)
Chọn B.







