Phương pháp giải:

Sử dụng công thức \(\frac{1}{6}SA.BC.d\left( SA;BC \right).\sin \widehat{\left( SA;BC \right)}\)

Lời giải chi tiết:

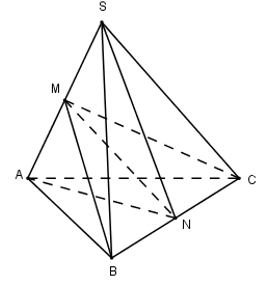
Gọi M, N lần lượt là trung điểm của SA và BC ta có:

\(\Delta SAB=\Delta SAC\left( c.c.c \right)\Rightarrow MB=MC\Rightarrow MN\bot BC\)

Tương tự ta chứng minh được \(MN\bot SA\)

\(\Rightarrow MN\) là đường vuông góc chung của SA và BC

\(\Rightarrow d\left( SA;BC \right)=MN\)

Xét tam giác SAB có :

\(B{{M}^{2}}=\frac{A{{B}^{2}}+S{{B}^{2}}}{2}-\frac{S{{A}^{2}}}{4}=\frac{{{y}^{2}}+{{z}^{2}}}{2}-\frac{{{x}^{2}}}{4}\)

Xét tam giác vuông MBN có :

\(MN=\sqrt{B{{M}^{2}}-B{{N}^{2}}}=\sqrt{\frac{{{y}^{2}}+{{z}^{2}}}{2}-\frac{{{x}^{2}}}{4}-\frac{{{x}^{2}}}{4}}=\sqrt{\frac{{{y}^{2}}+{{z}^{2}}-{{x}^{2}}}{2}}=\sqrt{\frac{9-2{{x}^{2}}}{2}}\)

Ta có: \({{V}_{S.ABCD}}=\frac{1}{6}SA.BC.d\left( SA;BC \right).\sin \widehat{\left( SA;BC \right)}=\frac{1}{6}{{x}^{2}}\sqrt{\frac{9-2{{x}^{2}}}{2}}\sin \widehat{\left( SA;BC \right)}\) đạt GTLN khi và chỉ khi  \(f\left( x \right)={{x}^{2}}\sqrt{\frac{9-2{{x}^{2}}}{2}}\) đạt GTLN và \(\sin \widehat{\left( SA;BC \right)}=1\)

Xét hàm số \(f\left( x \right)={{x}^{2}}\sqrt{\frac{9-2{{x}^{2}}}{2}}\,\,\left( 0<x\le \frac{3}{\sqrt{2}} \right)\) ta có:

\(\begin{array}{l}f'\left( x \right) = 2x\sqrt {\frac{{9 - 2{x^2}}}{2}}  + {x^2}\frac{{ - x}}{{\sqrt {\frac{{9 - 2{x^2}}}{2}} }} = \frac{{2x\frac{{9 - 2{x^2}}}{2} - {x^3}}}{{\sqrt {\frac{{9 - 2{x^2}}}{2}} }} = \frac{{ - 3{x^3} + 9x}}{{2\sqrt {\frac{{9 - 2{x^2}}}{2}} }} = 0 \Leftrightarrow x = \sqrt 3 \\f\left( {\sqrt 3 } \right) = \frac{{3\sqrt 6 }}{2}\\f\left( {\frac{3}{{\sqrt 2 }}} \right) = 0\\ \Rightarrow \mathop {\max }\limits_{\left( {0;\frac{3}{{\sqrt 2 }}} \right]} f\left( x \right) = \frac{{3\sqrt 6 }}{2}\\ \Rightarrow \max {V_{S.ABC}} = \frac{1}{6}.\frac{{3\sqrt 6 }}{2} = \frac{{\sqrt 6 }}{4}\end{array}\)

Chọn D.