Phương pháp giải:

+) Tỉ số \(\frac{{{V}_{1}}}{V}\) chính là tỉ số diện tích \(\frac{{{S}_{MBCDN}}}{{{S}_{ABCD}}}\).

+) \(\frac{{{S}_{MBCDN}}}{{{S}_{ABCD}}}=1-\frac{{{S}_{AMN}}}{{{S}_{ABCD}}}\)

+) Sử dụng BĐT \(ab\le {{\left( \frac{a+b}{2} \right)}^{2}}\,\,\left( a;b>0 \right)\)

Lời giải chi tiết:

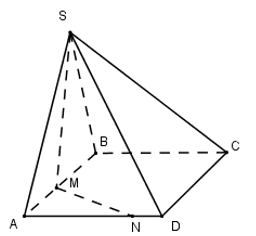
Đặt \(\frac{AB}{AM}=x;\frac{AD}{AN}=y\,\,\left( x,y>0 \right)\Rightarrow x+2y=4\)

Ta có: \(\frac{{{S}_{MBN}}}{{{S}_{ABCD}}}=\frac{\frac{1}{2}d\left( M;\left( AD \right).AN \right)}{d\left( B;AD \right).AD}=\frac{1}{2}\frac{AM}{AB}.\frac{AN}{AD}=\frac{1}{2xy}\)

\(\Rightarrow \frac{{{S}_{MBCDN}}}{{{S}_{ABCD}}}=1-\frac{1}{2xy}=\frac{{{V}_{S.MBCDN}}}{{{V}_{S.ABCD}}}=\frac{{{V}_{1}}}{V}\)

Áp dụng BĐT \(ab\le {{\left( \frac{a+b}{2} \right)}^{2}}\,\,\left( a,b>0 \right)\) cho hai số dương  x và 2y ta có: \(x.2y\le {{\left( \frac{x+2y}{2} \right)}^{2}}={{2}^{2}}=4\)

\(\Leftrightarrow 2xy\le 4\Leftrightarrow \frac{1}{2xy}\ge \frac{1}{4}\Leftrightarrow 1-\frac{1}{2xy}\le \frac{3}{4}\)

Vậy \(\max \frac{{{V}_{1}}}{V}=\frac{3}{4}\).

Chọn C.