Câu hỏi
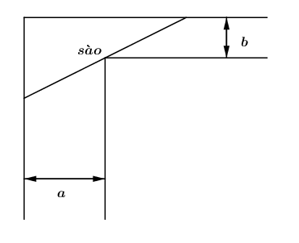
Để chặn đường hành lang hình chữ L, người ta dùng một que sào thẳng dài đặt kín những điểm chạm với hành lang (như hình vẽ). Biết rằng \(a=24\) và \(b=3\) , hỏi cái sào thỏa mãn điều kiện trên có chiều dài tối thiểu là bao nhiêu?
- A \(12\sqrt{5}\)
- B \(18\sqrt{5}\)
- C \(15\sqrt{5}\)
- D \(27\sqrt{5}\)
Lời giải chi tiết:
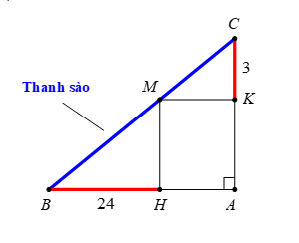
Theo bài ra, thanh sào sẽ đi qua các điểm \(B,\,\,M,\,\,C\) (hình vẽ dưới).
Suy ra độ dài thanh sào là \(L=BM+MC=\frac{BH}{\sin \widehat{BHM}}+\frac{CK}{\sin \widehat{CMK}}\)
Đặt \(\widehat{BMH}=x\,\,\Rightarrow \,\,\widehat{CMK}={{90}^{0}}-x,\) do đó \(L=\frac{24}{\sin x}+\frac{3}{\cos x}.\)
Yêu cầu bài toán \(\Leftrightarrow \,\,{{L}_{\min }}\Leftrightarrow \,\,f\left( x \right)=\frac{24}{\sin x}+\frac{3}{\cos x}\) min.
Ta có \({f}'\left( x \right)=\frac{3\sin x}{{{\cos }^{2}}x}-\frac{24\cos x}{{{\sin }^{2}}x}=0\Leftrightarrow {{\sin }^{3}}x=8{{\cos }^{3}}x\Leftrightarrow \tan x=2.\)
\(\Rightarrow \,\,\cos x=\frac{1}{\sqrt{1+{{\tan }^{2}}x}}=\frac{1}{\sqrt{5}}\Rightarrow \sin x=\sqrt{1-{{\cos }^{2}}x}=\frac{2}{\sqrt{5}}.\)
Suy ra \(\mathop {\min }\limits_{\left( {0;\frac{\pi }{2}} \right)} f\left( x \right) = 15\sqrt 5 .\) Vậy độ dài tối thiểu của thanh sào là \(15\sqrt{5}.\)
Chọn C







