Câu hỏi
Cho hình chóp S.ABC, đáy ABC là tam giác đều có độ dài cạnh bằng \(a\), SA vuông góc với đáy, \(SA=a\sqrt{3}\). Thể tích \(V\) của khối chóp S.ABC là
- A \(V=\frac{{{a}^{3}}}{2}\).
- B \(V=\frac{3{{a}^{3}}}{4}\).
- C \(V=\frac{{{a}^{3}}}{12}\).
- D \(V=\frac{{{a}^{3}}}{4}\).
Phương pháp giải:
Sử dụng công thức tính diện tích tam giác đều cạnh \(a\) là \(S=\frac{{{a}^{2}}\sqrt{3}}{4}\) và công thức tính thể tích khối chóp \(V=\frac{1}{3}h.S\).
Lời giải chi tiết:
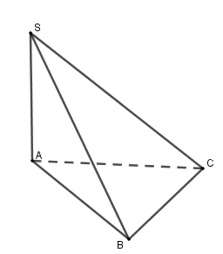
Vì tam giác \(ABC\) đều cạnh \(a\) nên \({{V}_{S.ABC}}=\frac{1}{3}SA.{{S}_{ABC}}=\frac{1}{3}a\sqrt{3}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}}{4}\).
Chọn D.
Câu hỏi trước
