Phương pháp giải:

Gắn hệ trục tọa độ đưa về tính thể tích khối tứ diện \({{V}_{MNPQ}}=\frac{1}{6}\left| \left[ \overrightarrow{MN},\overrightarrow{MP} \right].\overrightarrow{MQ} \right|\).

Lời giải chi tiết:

Gắn hệ trục tọa độ \(Oxyz\) với \(O\equiv {A}';Ox\equiv {A}'{B}';Oy\equiv {A}'A;Oz\equiv {A}'{D}'\)

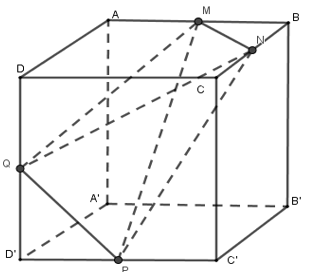
Ta có \({A}'\left( 0;0;0 \right);A\left( 0;1;0 \right);{B}'\left( 1;0;0 \right);{D}'\left( 0;0;1 \right),B\left( 1;1;0 \right),D\left( 0;1;1 \right),C\left( 1;1;1 \right),{C}'\left( 1;0;1 \right)\)

Vì \(M,N,P,Q\) là trung điểm của \(AB,BC,{C}'{D}',D{D}'\)nên \(M\left( \frac{1}{2};1;0 \right),N\left( 1;1;\frac{1}{2} \right);Q\left( 0;\frac{1}{2};1 \right);P\left( \frac{1}{2};0;1 \right)\)

Ta có \(\overrightarrow{MN}=\left( \frac{1}{2};0;\frac{1}{2} \right);\overrightarrow{MP}=\left( -\frac{1}{2};-\frac{1}{2};1 \right);\overrightarrow{MQ}=\left( 0;-1;1 \right)\)

\(\Rightarrow \left[ \overrightarrow{MN},\overrightarrow{MP} \right]=\left( \frac{1}{4};-\frac{3}{4};-\frac{1}{4} \right)\) \(\Rightarrow \left[ \overrightarrow{MN},\overrightarrow{MP} \right].\overrightarrow{MQ}=\frac{1}{2}\)

\({{V}_{MNPQ}}=\frac{1}{6}\left| \left[ \overrightarrow{MN},\overrightarrow{MP} \right].\overrightarrow{MQ} \right|\)\(=\frac{1}{12}\).

Chọn C.