Câu hỏi
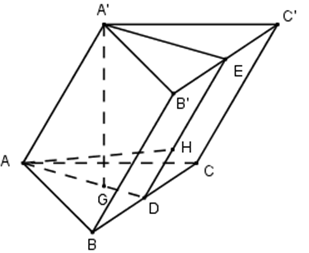
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A’ lên mặt phẳng (ABC) trùng với trọng tâm của tam giác ABC. Khoảng cách giữa hai đường thẳng AA’ và BC bằng \(\frac{3a}{4}\). Khi đó thể tích của khối lăng trụ là:
- A \(\frac{{{a}^{3}}\sqrt{3}}{4}\)
- B \(\frac{{{a}^{3}}\sqrt{3}}{3}\)
- C \(\frac{{{a}^{2}}\sqrt{3}}{2}\)
- D \(\frac{{{a}^{3}}\sqrt{3}}{12}\)
Phương pháp giải:
+) Gọi G là trọng tâm của tam giác ABC \(\Rightarrow A'G\bot \left( ABC \right)\)
+) \(d\left( AA';BC \right)=d\left( AA';\left( BCC'B' \right) \right)\)
+) Tính thể tích khối lăng trụ \({{V}_{ABC.A'B'C'}}=A'G.{{S}_{ABC}}\)
Lời giải chi tiết:
Gọi G là trọng tâm tam giác ABC \(\Rightarrow A'G\bot \left( ABC \right)\)
\(AA'//BB'\Rightarrow d\left( AA';BC \right)=d\left( AA';\left( BCC'C \right) \right)\)
Gọi D, E lần lượt là trung điểm của BC, B’C’ ta có:
\(\left\{ \begin{align} & BC\bot AD \\ & BC\bot A'G \\ \end{align} \right.\Rightarrow BC\bot \left( AA'ED \right)\Rightarrow \left( BCC'D' \right)\bot \left( AA'ED \right)\)
Trong (AA’ED) kẻ \(AH\bot DE\) ta có :
\(AH\bot \left( BCC'D' \right)\Rightarrow d\left( AA';BC \right)=AH=\frac{3a}{4}\)
Tam giác ABC đều cạnh a \(\Rightarrow AD=\frac{a\sqrt{3}}{2}\Rightarrow AG=\frac{a\sqrt{3}}{3}\)
\(\Rightarrow AA'=\sqrt{A'{{G}^{2}}+\frac{{{a}^{2}}}{3}}\)
Ta có:
\(\begin{align} & AH.AA'=A'G.AD\Leftrightarrow \frac{3a}{4}.\sqrt{A'{{G}^{2}}+\frac{{{a}^{2}}}{3}}=A'G.\frac{a\sqrt{3}}{2} \\ & \Leftrightarrow \frac{9}{16}\left( A'{{G}^{2}}+\frac{{{a}^{2}}}{3} \right)=\frac{3}{4}A'{{G}^{2}} \\ & \Leftrightarrow \frac{3}{16}A'{{G}^{2}}=\frac{3}{16}{{a}^{2}}\Rightarrow A'G=a \\ & {{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{4}\Rightarrow {{V}_{ABC.A'B'C'}}=A'G.{{S}_{ABC}}=a.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{3}}{4} \\ \end{align}\)
Chọn A.