Câu hỏi
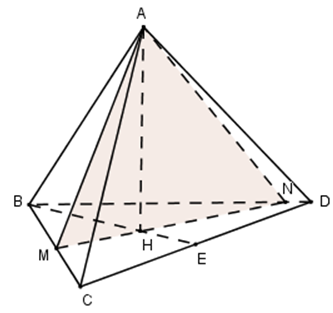
Cho tứ diện đều ABCD có cạnh đáy bằng 3. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD). Gọi V1, V2 lần lượt là giá trị lớn nhất và nhỏ nhất của thể tích khối tứ diện ABMN. Tính V1 + V2?
- A \(\frac{17\sqrt{2}}{8}\)
- B \(\frac{51\sqrt{2}}{16}\)
- C \(\frac{\sqrt{2}}{4}\)
- D \(\frac{51\sqrt{2}}{8}\)
Phương pháp giải:
Công thức tính thể tích khối chóp: \(V=\frac{1}{3}h{{S}_{d}}.\)
Lời giải chi tiết:
Tứ diện ABCD đều, gọi H là tâm tam giác đều BCD \(\Rightarrow AH\bot \left( BCD \right)\)
Có \(\left( AMN \right)\bot \left( BCD \right)\Rightarrow \left( AMN \right)\supset AH\Rightarrow H\in MN\)
\(\Rightarrow {{V}_{ABMN}}=\frac{1}{3}AH.{{S}_{BMN}}\), với AH không đổi.
Dễ thấy diện tích tam giác BMN nhỏ nhất khi và chỉ khi tam giác BMN đều, khi đó MN // CD
\(\frac{BM}{BC}=\frac{BH}{BE}=\frac{2}{3}\Rightarrow BM=\frac{2}{3}BC=2\Rightarrow {{S}_{BM{{N}_{\min }}}}=\frac{{{2}^{2}}\sqrt{3}}{4}=\sqrt{3}\)
Diện tích tam giác BMN lớn nhất khi và chỉ khi \(N\equiv D\) hoặc \(M\equiv C\) , khi đó \({{S}_{BM{{N}_{\max }}}}=\frac{1}{2}{{S}_{ABC}}=\frac{1}{2}\frac{{{3}^{2}}\sqrt{3}}{4}=\frac{9\sqrt{3}}{8}\)
Có \(BH=\frac{2}{3}BE=\frac{2}{3}.\frac{3\sqrt{3}}{2}=\sqrt{3}\Rightarrow AH=\sqrt{A{{B}^{2}}-B{{H}^{2}}}=\sqrt{{{3}^{2}}-{{\left( \sqrt{3} \right)}^{2}}}=\sqrt{6}\)
\(\begin{align} & \Rightarrow {{V}_{1}}=\frac{1}{3}AH.{{S}_{BM{{N}_{\text{max}}}}}=\frac{1}{3}\sqrt{6}.\frac{9\sqrt{3}}{8}=\frac{9\sqrt{2}}{8} \\ & \,\,\,\,\,\,{{V}_{2}}=\frac{1}{3}AH.{{S}_{BM{{N}_{\text{min}}}}}=\frac{1}{3}\sqrt{6}.\sqrt{3}=\sqrt{2} \\ & \Rightarrow {{V}_{1}}+{{V}_{2}}=\frac{17\sqrt{2}}{8} \\ \end{align}\)
Chọn A.