Phương pháp giải:

- Tìm các điểm cực trị của đồ thị hàm số.

- Tính diện tích tam giác theo công thức \(S=\frac{1}{2}ah\)

Lời giải chi tiết:

\(\begin{array}{l}y = {x^4} - 2{x^2} + 2\,\,(C) \Rightarrow y' = 4{x^3} - 4x\\y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\end{array}\)

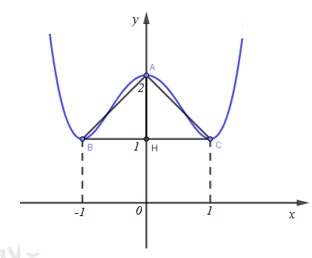
Tọa độ các điểm cực trị của (C) là: \(A(0;2),\,\,B(-1;1),\,C(1;1)\).

Diện tích tam giác ABC:  \({{S}_{ABC}}=\frac{1}{2}AH.BC=\frac{1}{2}.(2-1).(1-(-1))=1\)

Chọn: C.