Phương pháp giải:

- Biểu diễn được góc giữa (SBC) và (ABCD).

- Tính thể tích khối chóp S.ABCD.

- Lập tỉ số thể tích giữa các khối chóp\(S.AGD\) và \(S.ADI\), giữa các khối chóp \(S.ADI\) và \(S.ABCD\).  Từ đó tính thể tích khối chóp S.AGD.

Lời giải chi tiết:

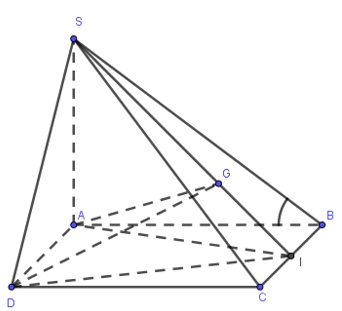
Ta có:

\(\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB\)

\(\begin{array}{l}\left\{ \begin{array}{l}(SBC) \cap (ABCD) = BC\\(SBC) \cap (SAB) = SB \bot BC\\(ABCD) \cap (SAB) = AB \bot BC\end{array} \right.\\ \Rightarrow \left( {\widehat {(SBC);(ABCD)}} \right) = \left( {\widehat {AB;SB}} \right) = \widehat {SBA} = {60^0}\end{array}\)

 Tam giác SAB vuông tại A:  \(\tan \widehat{SBA}=\frac{SA}{AB}\Leftrightarrow \tan {{60}^{0}}=\frac{2a}{AB}\Rightarrow AB=\frac{2a}{\sqrt{3}}\)

Thể tích khối chóp S.ABCD:  \({{V}_{S.ABCD}}=\frac{1}{3}.SA.{{S}_{ABCD}}=\frac{1}{3}.SA.AB.AD=\frac{1}{3}.2a.\frac{2a}{\sqrt{3}}.2a=\frac{8\sqrt{3}{{a}^{3}}}{9}\)

Ta có: \(\frac{{{V}_{S.AGD}}}{{{V}_{S.AID}}}=\frac{SG}{SI}=\frac{2}{3}\) (vì G là trọng tâm tam giác SBC)

Mà \(\frac{{{V}_{S.AID}}}{{{V}_{S.ABCD}}}=\frac{{{S}_{AID}}}{{{S}_{ABCD}}}=\frac{1}{2}\)

\(\Rightarrow \frac{{{V}_{S.AGI}}}{{{V}_{S.ABCD}}}=\frac{2}{3}.\frac{1}{2}=\frac{1}{3}\Rightarrow {{V}_{S.AGI}}=\frac{1}{3}{{V}_{S.ABCD}}=\frac{1}{3}.\frac{8\sqrt{3}{{a}^{3}}}{9}=\frac{8\sqrt{3}{{a}^{3}}}{27}\)

Chọn: B.