Câu hỏi
Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng \(2a\). Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm b . Đặt \(\alpha \) là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây đúng?
- A \(\tan \alpha =\sqrt{2}\).
- B \(\tan \alpha =\frac{1}{\sqrt{2}}\).
- C \(\tan \alpha =\frac{1}{2}\).
- D \(\tan \alpha =1\).
Phương pháp giải:
- Trên (O), (O’) lần lượt lấy B’, A’ sao cho AA’ // BB’ // OO’.
- Xác định góc \(\alpha \): góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính thể tích khối tứ diện \(OO'AB\) theo thể tích khối lăng trụ \(OAB'.O'A'B\).
- Tìm GTLN của khối lăng trụ suy ra số đo góc \(\widehat{AOB'}={{90}^{0}}\Rightarrow A'B=AB'=a\sqrt{2}\Rightarrow \tan \alpha \)
Lời giải chi tiết:
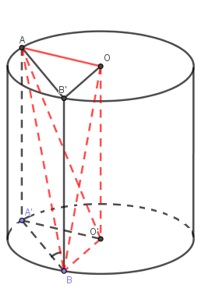
Trên (O), (O’) lần lượt lấy B’, A’ sao cho AA’ // BB’ // OO’.
Ta có: \(\left\{ \begin{array}{l}AA' \bot (O'A'B)\\AB \cap (O'A'B) = \left\{ B \right\}\end{array} \right. \Rightarrow \left( {\widehat {AB,(O'A'B)}} \right) = \left( {\widehat {AB,A'B}} \right) = \widehat {ABA'} = \alpha \)
Ta có: OAB’.O’A’B là hình lăng trụ.
\({{V}_{OO'AB}}=\frac{1}{2}{{V}_{A.OO'BB'}}=\frac{1}{2}.\left( {{V}_{OAB'.O'A'B}}-{{V}_{A.A'BO'}} \right)=\frac{1}{2}\left( V-\frac{V}{3} \right)=\frac{V}{3}\)
(V: thể tích lăng trụ OAB’.O’A’B)
\(\Rightarrow {{V}_{OO'AB}}\) đạt giá trị lớn nhất khi và chỉ khi \(V\)lớn nhất.
Mà, thể tích lăng trụ:
\(V={{S}_{OAB'}}.OO'=\frac{1}{2}.OA.OB'\sin \widehat{O}.\,OO'=\frac{1}{2}.2a.2a.\sin \widehat{O}.2a=4{{a}^{3}}.\sin \widehat{O}\le 4{{a}^{3}}\)
\(\Rightarrow {{V}_{\max }}=4{{a}^{3}}\) khi và chỉ khi \(\widehat{AOB'}={{90}^{0}}\)
\(\begin{array}{l} \Rightarrow AB' = OA\sqrt 2 = 2a\sqrt 2 \\ \Rightarrow \tan \alpha = \frac{{AA'}}{{A'B}} = \frac{{2a}}{{2a\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\end{array}\)
Chọn: B.







