Phương pháp giải:

- Lập tỉ số thể tích thông qua tỉ số diện tích đáy và tỉ số đường cao.

Lời giải chi tiết:

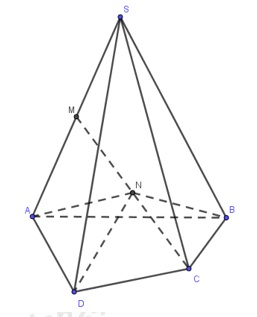
Ta có:

\(\frac{{{V_{N.ABCD}}}}{{{V_{M.ABCD}}}} = \frac{{d(N,(ABCD))}}{{d(M,(ABCD))}} = \frac{{NC}}{{MC}} = \frac{1}{2} \Rightarrow {V_{N.ABCD}} = \frac{1}{2}{V_{M.ABCD}}\)

\(\begin{array}{l}\frac{{{V_{M.ABCD}}}}{{{V_{S.ABCD}}}} = \frac{{d(M,(ABCD))}}{{d(S,(ABCD))}} = \frac{{MA}}{{SA}} = \frac{1}{2} \Rightarrow {V_{M.ABCD}} = \frac{1}{2}{V_{S.ABCD}} = \frac{1}{2}V\\ \Rightarrow {V_{N.ABCD}} = \frac{1}{2}.\frac{1}{2}.V = \frac{1}{4}V\end{array}\)

Chọn: B.