Phương pháp giải:

- Sử dụng phương pháp đồ thị hàm số để đánh giá.

Lời giải chi tiết:

                     \({{x}^{3}}-3{{x}^{2}}-{{m}^{3}}+3{{m}^{2}}=0\Leftrightarrow {{x}^{3}}-3{{x}^{2}}={{m}^{3}}-3{{m}^{2}}\,\,(*)\)

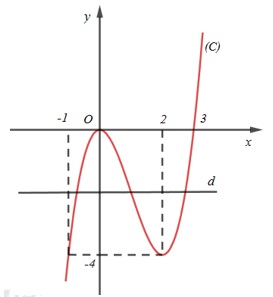
Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}\,\,(C)\) và đường thẳng\(y={{m}^{3}}-3{{m}^{2}}\,\,\,(d)\).

Quan sát đồ thị, ta có:

(C) cắt (d) tại 3 điểm phân biệt khi và chỉ khi \(-4<{{m}^{3}}-3{{m}^{2}}<0\)

\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
{m^3} - 3{m^2} + 4 > 0\\
{m^3} - 3{m^2} < 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{\left( {m - 2} \right)^2}\left( {m + 1} \right) > 0\\
{m^2}\left( {m - 3} \right) < 0
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
m + 1 > 0\\
m - 2 \ne 0\\
m - 3 < 0\\
m \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
m > - 1\\
m \ne 2\\
m < 3\\
m \ne 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
- 1 < m < 3\\
m \ne 0\\
m \ne 2
\end{array} \right..
\end{array}\)

(Cũng do quan sát được từ đồ thị hàm số (C): xác định các giá trị của x để hàm số \(y={{x}^{3}}-3{{x}^{2}}\) có giá trị từ - 4 đến 0).

Vậy  \(\left\{ \begin{array}{l}- 1 < m < 3\\m \ne 2\\m \ne 0\end{array} \right..\)

Chọn: B.