Phương pháp giải:

- Vẽ đồ thị hàm số \(y={{x}^{4}}-3{{x}^{2}}-2\) và tìm giao điểm của đồ thị hàm số với đường thẳng \(y=m>0\)

- Điều kiện để tam giác \(OAB\) vuông tại \(O\) là b  thuộc tia phân giác góc phần tư thứ \(\left( II \right)\).

Lời giải chi tiết:

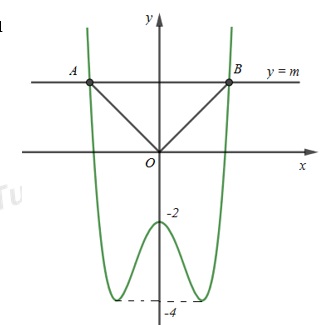
- Quan sát đồ thị hàm số, ta thấy: với mọi m > 0, đồ thị hàm số \(y={{x}^{4}}-3{{x}^{2}}-2\) luôn cắt đường thẳng \(y=m\) tại hai điểm phân biệt.

Giả sử tọa độ điểm \(A({{x}_{1}};{{y}_{1}}),\,\,B({{x}_{2}};{{y}_{2}}),\,\,{{x}_{1}}<{{x}_{2}}\)

Dễ dàng chứng minh tam giác OAB cân tại O.

Mà, theo đề bài, ta có: Tam giác OAB vuông tại O, suy ra OAB vuông cân tại O

\(\Rightarrow OB\) là tia phân giác của góc phần tư thứ I

\(B\)thuộc đường thẳng \(y=x\) và B có tung độ dương.

 Xét phương trình hoành độ giao điểm của \(y={{x}^{4}}-3{{x}^{2}}-2\) và đường thẳng \(y=x\):

                              \(\begin{array}{l}{x^4} - 3{x^2} - 2 = x \Leftrightarrow {x^4} - 3{x^2} - x - 2 = 0 \Leftrightarrow (x - 2)({x^3} + 2{x^2} + x + 1) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\{x^3} + 2{x^2} + x + 1 = 0(2)\end{array} \right.\end{array}\)

Ta thấy, với x > 0, \({{x}^{3}}+2{{x}^{2}}+x+1>0\Rightarrow (2)\) không có nghiệm \(x>0\).

Vậy, phương trình (1) có duy nhất một nghiệm dương là \(x=2\Rightarrow B(2;2)\Rightarrow m=2\).

Chọn: A.