Câu hỏi
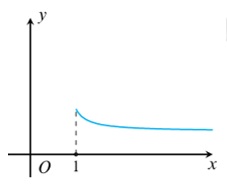
Hỏi có bao nhiêu cặp số nguyên dương\(\left( a;b \right)\) để hàm số \(y=\frac{2x-a}{4x-b}\) có đồ thị trên \(\left( 1;+\infty \right)\) như hình vẽ bên?
- A 1
- B 4
- C 2
- D 3
Phương pháp giải:
Quan sát và nhận xét đồ thị, tìm điều kiện để hàm số nghịch biến trên \(\left( 1;+\infty \right)\)
- Thử từng giá trị của b và suy ra kết luận.
Lời giải chi tiết:
Quan sát đồ thị, ta thấy: đồ thị hàm số \(y=\frac{2x-a}{4x-b}\) nghịch biến trên \(\left( 1;+\infty \right)\).
Ta có: \(y=\frac{2x-a}{4x-b}\Rightarrow y'=\frac{4a-2b}{{{(4x-b)}^{2}}},\,\,x\ne \frac{b}{4}\)
Lại có, đồ thị hàm số cắt đường thẳng \(x=1\) nên \(x=1\) không là tiệm cận đứng của đồ thị hàm số.
Suy ra \(\frac{b}{4}\ne 1\Leftrightarrow b\ne 4\)
Để hàm số \(y=\frac{2x-a}{4x-b}\) nghịch biến trên \(\left( 1;+\infty \right)\) thì \(\left\{ \begin{array}{l}4a - 2b < 0\\\frac{b}{4} < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b > 2a\\b < 4\end{array} \right.\)
\(b\in {{\mathbb{Z}}^{+}}\Rightarrow b\in \left\{ 1;2;3 \right\}\)
+) \(b=1\Rightarrow 1>2a\Rightarrow a<\frac{1}{2}\): Không có giá trị của a thỏa mãn.
+) \(b=2\Rightarrow 2>2a\Rightarrow a<1\): Không có giá trị của a thỏa mãn.
+) \(b=3\Rightarrow 3>2a\Rightarrow a<\frac{3}{2}\Rightarrow a=1\Rightarrow y=\frac{2x-1}{4x-3}\) thỏa mãn bài toán.
Vậy, có tất cả \(1\) cặp số nguyên dương \(\left( a;b \right)\) thỏa mãn yêu cầu đề bài là: \(\left( 1;3 \right)\).
Chọn: A.







