Phương pháp giải:

\({{V}_{non}}=\frac{1}{3}Sh=\frac{1}{3}\pi {{R}^{2}}h\), trong đó S: diện tích đáy, R: bán kính đáy, h: độ dài đường cao.

Lời giải chi tiết:

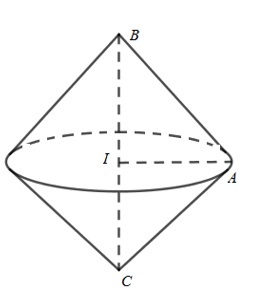
Khi quay hình tam giác ABC quanh trục BC ta thu được khối tròn xoay là 2 khối nón ghép lại với nhau.

Thể tích khối tròn xoay là:

\(V=\frac{1}{3}S.BI+\frac{1}{3}S.CI=\frac{1}{3}S.(BI+CI)=\frac{1}{3}S.BC\)

(Trong đó, S: là diện tích hình tròn tâm I bán kính IA)

                         \( = \frac{1}{3}.I{A^2}.\pi .BC = \frac{1}{3}.{\left( {\frac{{BC}}{2}} \right)^2}\pi .BC = \frac{1}{3}.{\left( {\frac{2}{2}} \right)^2}.\pi .2 = \frac{{2\pi }}{3}\)

Chọn: C.