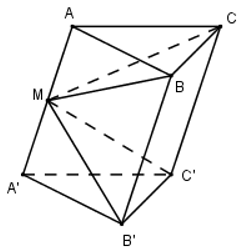
Câu hỏi
Cho khối lăng trụ ABC.A’B’C’ có thể tích V. Điểm M là trung điểm cạnh AA’. Thính theo V thể tích khối chóp M.BCC’B’.
- A \(\frac{2V}{3}\)
- B \(\frac{3V}{4}\)
- C \(\frac{V}{3}\)
- D \(\frac{V}{2}\)
Phương pháp giải:
\({{V}_{M.BCC'B'}}={{V}_{ABC.A'B'C'}}-{{V}_{M.ABC}}-{{V}_{M.A'B'C'}}\)
Lời giải chi tiết:
Ta có: \({{V}_{M.BCC'B'}}={{V}_{ABC.A'B'C'}}-{{V}_{M.ABC}}-{{V}_{M.A'B'C'}}\)
\({{V}_{M.ABC}}=\frac{1}{3}d\left( M;\left( ABC \right) \right).{{S}_{ABC}}=\frac{1}{3}.\frac{1}{2}d\left( A';\left( ABC \right) \right).{{S}_{ABC}}=\frac{1}{6}{{V}_{ABC.A'B'C'}}\)
Tương tự ta có: \({{V}_{M.A'B'C'}}=\frac{1}{6}V\)
\(\Rightarrow {{V}_{M.BCC'B'}}=V-\frac{V}{6}-\frac{V}{6}=\frac{2V}{3}\)
Chọn A.
Câu hỏi trước
