Câu hỏi
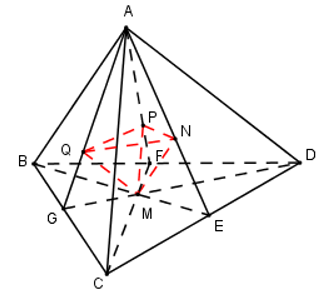
Cho tứ diện ABCD có thể tích là V. Điểm M thay đổi trong tam giác BCD. Các đường thẳng đi qua M và song song với AB, AC, AD lần lượt cắt các mặt phẳng (ACD), (ABD), (ABC) tại N, P, Q. Giá trị lớn nhất của thể tích khối MNPQ là:
- A \(\frac{V}{27}\)
- B \(\frac{V}{16}\)
- C \(\frac{V}{8}\)
- D \(\frac{3V}{54}\)
Phương pháp giải:
Áp dụng công thức tính thể tích của tứ diện vuông.
Lời giải chi tiết:
Giả sử tứ diện ABCD có AB, AC, AD đôi một vuông góc \(\Rightarrow {{V}_{ABCD}}=\frac{AB.AC.AD}{6}.\)
Khi đó, tứ diện MNPQ có MN, MP, MQ đôi một vuông góc \(\Rightarrow {{V}_{MNPQ}}=\frac{MN.MP.MQ}{6}.\)
Ta chứng minh được \(\frac{MN}{AB}+\frac{MP}{AC}+\frac{MQ}{AD}=1\) (dựa vào định lý Ta-let), khi đó:
\(\begin{align} & MN.MP.MQ=AB.AC.AD.\frac{MN}{AB}.\frac{MP}{AC}.\frac{MQ}{AD} \\ & \le AB.AC.AD.\frac{{{\left( \frac{MN}{AB}+\frac{MP}{AC}+\frac{MQ}{AD} \right)}^{3}}}{27} \\ & =\frac{AB.AC.AD}{27}. \\ \end{align}\)
Vậy \({{V}_{MNPQ}}=\frac{MN.MP.MQ}{6}\le \frac{1}{27}.\frac{AB.AC.AD}{6}=\frac{V}{27}.\)
\(\Rightarrow {{V}_{\max }}=\frac{V}{27}.\)
Chọn A.