Câu hỏi
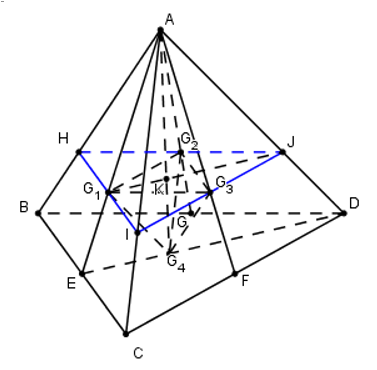
Cho khối tứ diện ABCD có thể tích là V. Gọi \({{G}_{1}},{{G}_{2}},{{G}_{3}},{{G}_{4}}\) là trọng tâm của 4 mặt của tứ diện ABCD. Thể tích khối tứ diện \({{G}_{1}}{{G}_{2}}{{G}_{3}}{{G}_{4}}\) là:
- A \(\frac{V}{27}\)
- B \(\frac{V}{18}\)
- C \(\frac{V}{4}\)
- D \(\frac{V}{12}\)
Phương pháp giải:
Xác định thiết diện của mặt phẳng \(\left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right)\) với tứ diện ABCD. Sử dụng các tỉ số và chiều cao và diện tích đáy để suy ra tỉ số thể tích của các khối chóp.
Lời giải chi tiết:
Ta có: \(\left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right)\) và (ABC) có điểm \({{G}_{1}}\) chung và \({{G}_{2}}{{G}_{3}}//GF//BC\) nên giao tuyến của hai mặt phẳng là HI đi qua G1 và song song với BC.
Tương tự ta chứng minh được:
\(\begin{align} & \left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right)\cap \left( ABD \right)=HJ//BD \\ & \left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right)\cap \left( ACD \right)=IJ//CD \\ & \Rightarrow \left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right)\equiv \left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right) \\ \end{align}\)
Trong (AED): \(A{{G}_{4}}\cap J{{G}_{1}}=K\Rightarrow A{{G}_{4}}\cap \left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right)=K\)
\(\Rightarrow \frac{d\left( {{G}_{4}};\left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right) \right)}{d\left( A;\left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right) \right)}=\frac{{{G}_{4}}K}{AK}\)
Ta có:
\(\frac{A{{G}_{1}}}{AE}=\frac{AH}{AB}=\frac{AJ}{AD}=\frac{2}{3}\Rightarrow {{G}_{1}}J//ED\Rightarrow \frac{{{G}_{4}}K}{AK}=\frac{E{{G}_{1}}}{A{{G}_{1}}}=\frac{1}{2}\)\(\Rightarrow {{V}_{{{G}_{4}}.{{G}_{1}}{{G}_{2}}{{G}_{3}}}}=\frac{1}{3}d\left( {{G}_{4}};\left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right) \right).{{S}_{{{G}_{1}}{{G}_{2}}{{G}_{3}}}}=\frac{1}{3}.\frac{1}{2}d\left( A;\left( {{G}_{1}}{{G}_{2}}{{G}_{3}} \right) \right).{{S}_{{{G}_{1}}{{G}_{2}}{{G}_{3}}}}=\frac{1}{2}{{V}_{A.{{G}_{1}}{{G}_{2}}{{G}_{3}}}}\)
Dễ dàng chứng minh được \(\Delta {{G}_{1}}{{G}_{2}}{{G}_{3}}\backsim \Delta JIH\) theo tỉ số \(k=\frac{1}{2}\Rightarrow {{S}_{{{G}_{1}}{{G}_{2}}{{G}_{3}}}}=\frac{1}{4}{{S}_{HIJ}}\Rightarrow {{V}_{A.{{G}_{1}}{{G}_{2}}{{G}_{3}}}}=\frac{1}{4}{{V}_{A.HIJ}}\)
\(\begin{align} & \frac{{{V}_{A.HIJ}}}{{{V}_{A.BCD}}}=\frac{AH}{AB}.\frac{AI}{AC}.\frac{AJ}{AD}={{\left( \frac{2}{3} \right)}^{3}}=\frac{8}{27}\Rightarrow {{V}_{A.HIJ}}=\frac{8}{27}{{V}_{A.BCD}} \\ & \Rightarrow {{V}_{{{G}_{4}}.{{G}_{1}}{{G}_{2}}{{G}_{3}}}}=\frac{1}{2}.\frac{1}{4}.\frac{8}{27}=\frac{1}{27}V \\ \end{align}\)
Chọn A.