Phương pháp giải:

+) Chia khối tám mặt đều thành hai khối chóp tứ diện đều.

+) Tính thể tích khối chóp tứ diện đều bởi công thức: \(V=\frac{1}{3}h{{S}_{d}}.\)

Lời giải chi tiết:

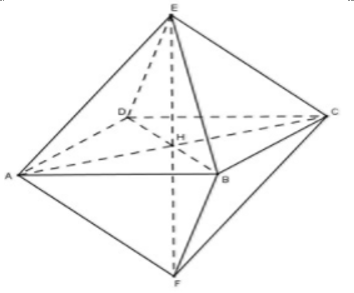
Chia khối tam mặt đều cạnh a thành hai khối chóp tứ diện đều cạnh a.

Khi đó ta có EH là chiều cao của khối chóp EABCD.

Ta có: \({{V}_{EABC\text{D}F}}=2{{V}_{EABCD}}.\)

Gọi h là chiều cao của khối chóp ta được:

\(\begin{align}  & {{h}^{2}}={{a}^{2}}-{{\left( \frac{a\sqrt{2}}{2} \right)}^{2}}=\frac{{{a}^{2}}}{2}\Rightarrow h=\frac{a\sqrt{2}}{2}. \\  & \Rightarrow {{V}_{EABCDF}}=2{{V}_{EABCD}}=2.\frac{1}{3}.\frac{a\sqrt{2}}{2}.{{a}^{2}}=\frac{{{a}^{3}}\sqrt{2}}{3}. \\ \end{align}\)

Chọn C.