Câu hỏi
Cho khối chóp S.ABC có \(SA\bot (ABC),\,\,SA=a,\,\,AB=a,\,\,AC=2a\) và \(\widehat{BAC}={{120}^{0}}\). Tính thể tích khối chóp S.ABC.
- A \(\frac{{{a}^{3}}\sqrt{3}}{3}.\)
- B \(\frac{{{a}^{3}}\sqrt{3}}{2}.\)
- C \(\frac{{{a}^{3}}\sqrt{3}}{6}.\)
- D \({{a}^{3}}\sqrt{3}.\)
Lời giải chi tiết:
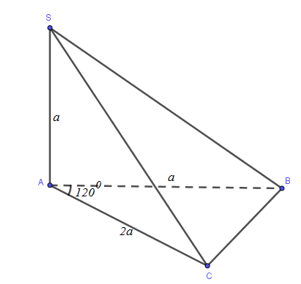
Thể tích khối chóp S.ABC :
\({{V}_{S.ABC}}=\frac{1}{3}SA.\,\,{{S}_{ABC}}=\frac{1}{3}.SA.\frac{1}{2}.AB.AC.\sin A=\frac{1}{3}.a.\frac{1}{2}.a.2a.\sin {{120}^{0}}=\frac{{{a}^{3}}\sqrt{3}}{6}\)
Chọn: C.
Câu hỏi trước
