Phương pháp giải:

- Tính tỉ số thể tích thông qua tỉ số đường cao và tỉ số diện tích đáy tương ứng.

Lời giải chi tiết:

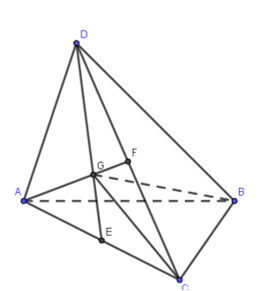
Gọi E là trung điểm của AC.

Vì G là trọng tâm tam giác ACD nên \(\frac{GE}{DE}=\frac{1}{3}\).

Ta có: \(\left\{ \begin{array}{l}DE \cap (ABC) = E\\G \in DE\\\frac{{GE}}{{DE}} = \frac{1}{3}\end{array} \right. \Rightarrow \frac{{d(G,(ABC))}}{{d(D,(ABC))}} = \frac{1}{3}\)

\(\frac{{{V}_{G.ABC}}}{{{V}_{ABCD}}}=\frac{d(G,(ABC))}{d(D,(ABC))}=\frac{1}{3}\Rightarrow {{V}_{G.ABC}}=\frac{{{V}_{ABCD}}}{3}=\frac{V}{3}\) 

Chọn: D.