Câu hỏi
Cho khối nón có bán kính đáy r = 3 (cm) và góc ở đỉnh \({{120}^{0}}\). Tính diện tích xung quanh \({{S}_{xq}}\)của khối nón đó.
- A \(9\pi \,(c{{m}^{2}}).\)
- B \(3\pi \sqrt{3}\,(c{{m}^{2}}).\)
- C \(6\pi \sqrt{3}\,(c{{m}^{2}}).\)
- D \(\sqrt{3}\pi \,(c{{m}^{2}}).\)
Phương pháp giải:
Diện tích xung quanh của khối nón: \({{S}_{xq}}=\pi rl\)
( Trong đó, \(r:\) bán kính đường tròn đáy, \(l\): độ dài đường sinh).
Lời giải chi tiết:
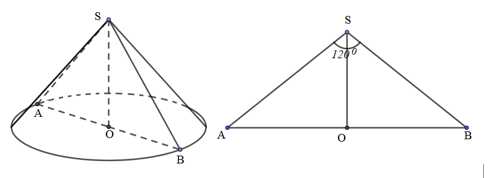
Áp dụng định lý Côsin cho tam giác SAB:
\(A{{B}^{2}}=S{{A}^{2}}+S{{B}^{2}}-2.SA.SB.\cos A\Leftrightarrow {{(2.3)}^{2}}={{l}^{2}}+{{l}^{2}}-2.l.l.\cos {{120}^{0}}\Leftrightarrow 3{{l}^{2}}=36\Leftrightarrow l=2\sqrt{3}\)
Diện tích xung quanh của khối nón: \({{S}_{xq}}=\pi rl=\pi .3.2\sqrt{3}=6\sqrt{3}\pi \,(c{{m}^{2}})\)
Chọn: C.
Câu hỏi trước
