Câu hỏi
Cho hình nón có chiều cao \(a\sqrt{3}\)và bán kính đáy \(a\). Tính diện tích xung quanh \({{S}_{xq}}\)của hình nón.
- A \({{S}_{xq}}=2\pi {{a}^{2}}.\)
- B \({{S}_{xq}}=\pi {{a}^{2}}.\)
- C \({{S}_{xq}}=\frac{\pi {{a}^{2}}}{2}.\)
- D \({{S}_{xq}}=4\pi {{a}^{2}}.\)
Phương pháp giải:
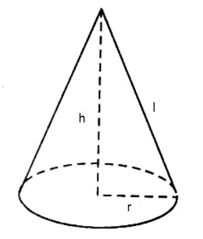
- Mối liên hệ giữa đường cao, bán kính đáy và độ dài đường sinh của hình nón:
\({{h}^{2}}+{{r}^{2}}={{l}^{2}}\)
- Diện tích xung quanh của hình nón: \({{S}_{xq}}=\pi rl\)
(Trong đó, \(r:\) bán kính đáy, \(l:\)độ dài đường sinh, h: độ dài đường cao).
Lời giải chi tiết:
Ta có: \({{h}^{2}}+{{r}^{2}}={{l}^{2}}\Leftrightarrow {{\left( a\sqrt{3} \right)}^{2}}+{{a}^{2}}={{l}^{2}}\Leftrightarrow l=2a\)
Diện tích xung quanh của hình nón: \({{S}_{xq}}=\pi rl=\pi a.2a=2\pi {{a}^{2}}\)
Chọn: A.







