Môn Lý - Lớp 12
40 bài tập Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ Frenen mức độ vận dụng
Câu hỏi
Cho bốn dao động điều cùng phương cùng tần số góc có phương trình lần lượt là:
\({x_1} = 10\cos \left( {20\pi t + \frac{\pi }{3}} \right)cm;{x_2} = 6\sqrt 3 \cos (20\pi t)cm\) và:
\({x_3} = 4\sqrt 3 \cos \left( {20\pi t - \frac{\pi }{2}} \right)cm;{x_4} = 10\cos \left( {20\pi t + \frac{{2\pi }}{3}} \right)cm\).
Một vật có khối lượng 500 g thực hiện đồng thời bốn dao động trên. Xác định thời điểm vật qua li độ \(x = - 3\sqrt 6 cm\) lần thứ 9?
- A 0,421 s
- B 4,21 s
- C 0,0421 s.
- D 0,00421 s
Phương pháp giải:
Sử dụng máy tính casio.
Lời giải chi tiết:
Cài đặt máy tính ở chế độ số phức MODE 2
Ta có x = x1 + x2 + x3 + x4, bấm máy
\(10\angle {\pi \over 3} + 6\sqrt 3 \angle 0 + 4\sqrt 3 \angle - {\pi \over 2} + 10\angle {{2\pi } \over 3}SHIFT23 = \)
Đọc kết quả \(6\sqrt 6 \angle {\pi \over 4}\)
Vậy phương trình dao động tổng hợp là \(x = 6\sqrt 6 \cos s\left( {20\pi t + {\pi \over 4}} \right)cm\)
Chu kì dao động T = 2π/ω = 0,1s
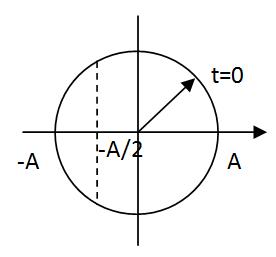
Ta có đường tròn lượng giác
Từ hình vẽ ta thấy thời gian để vật đi qua vị trí \(x = - 3\sqrt 6 cm\) lần thứ 9 là
\(t = 4T + {T \over 8} + {T \over {12}} = 0,421{\rm{s}}\)
Chọn A
Câu hỏi trước
