Câu hỏi
Cho hàm số \(f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d\)\(\left( a,b,c,d\in \mathbb{R},a\ne 0 \right)\)có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?
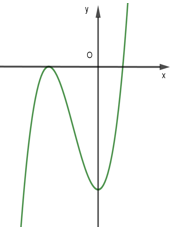
- A \(a>0;b>0;c>0;d<0\)
- B \(a<0;b<0;c=0;d<0\)
- C \(a>0;b>0;c=0;d<0\)
- D \(a>0;b<0;c=0;d<0\)
Phương pháp giải:
Sử dụng cách đọc đồ thị hàm số.
Lời giải chi tiết:
Ta có : \(f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d\); \(f'(x)=3a{{x}^{2}}+2bx+c\)
Do \(f(x)\to +\infty \) khi \(x\to +\infty \) nên \(a>0\)
Do đồ thị hàm số\(f(x)\) có hai điểm cực trị là \(\left( {{x}_{0}};0 \right)\) và \(\left( 0;{{y}_{0}} \right)\) với \({{x}_{0}}<0\) và \({{y}_{0}}<0\)
Nên : \(\left\{ \begin{array}{l}f(0) = {y_0} < 0\\f\left( {{x_0}} \right) = 0\\f'\left( 0 \right) = 0\\f'\left( {{x_0}} \right) = 0\end{array} \right.\) Ta có : \(\left\{ \begin{array}{l}f(0) = d\\f'(0) = c\end{array} \right. \Rightarrow \left\{ \begin{array}{l}d < 0\\c = 0\end{array} \right.\) ;
+ \(f'\left( {{x}_{0}} \right)=0\)\(\Leftrightarrow 3a{{x}_{0}}^{2}+2b{{x}_{0}}=0\)\(\Leftrightarrow {{x}_{0}}=\frac{-2b}{3a}\) Mà \({{x}_{0}}<0\);\(a>0\) \(\Rightarrow b>0\)
Vậy, \(a>0;b>0;c=0;d<0\)
Chọn C.







