Câu hỏi
Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\), \(\left( a,b,c\in \mathbb{R},a\ne 0 \right)\) có đồ thị \(\left( C \right)\) Biết rằng \(\left( C \right)\) không cắt trục \(Ox\) và có đồ thị hàm số \(y={f}'\left( x \right)\) như hình vẽ.
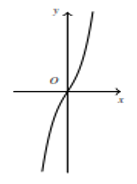
Hàm số đã cho có thể là hàm số nào trong các hàm số dưới đây ?
- A \(y=-4{{x}^{4}}-{{x}^{2}}-1\)
- B \(y=2{{x}^{4}}-{{x}^{2}}+2\) .
- C \(y={{x}^{4}}+{{x}^{2}}-2\) .
- D \(y=\frac{1}{4}{{x}^{4}}+{{x}^{2}}+1\)
Phương pháp giải:
Dựa vào đồ thị của hàm \({f}'\left( x \right)\) ta suy ra các tính chất \({f}'\left( x \right)=0\) có một nghiệm duy nhất \(x=0\) và \({f}'\left( x \right)\) đổi dấu từ âm sang dương nên \(x=0\) là điểm cực tiểu của đồ thị hàm số.
Lời giải chi tiết:
Dựa vào đồ thị hàm số \(y={f}'\left( x \right)\) ta thấy phương trình \({f}'\left( x \right)=0\) chỉ có nghiệm duy nhất \(x=0\) và \(y={f}'\left( x \right)\) đổi dấu từ âm sang dương khi đi qua \(x=0\)nên hàm số \(y=f\left( x \right)\)có duy nhất một cực trị là cực tiểu.
A. \(y=-4{{x}^{4}}-{{x}^{2}}-1\) có \({y}'\left( 0 \right)=-16{{x}^{3}}-2x=0,{{y}'}'\left( 0 \right)=-48{{x}^{2}}-2<0\) nên \(x=0\) là điểm cực đại.
B. \(y=2{{x}^{4}}-{{x}^{2}}+2\) có \(y' = 8{x^3} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \frac{1}{2}\end{array} \right.\).
C. \(y={{x}^{4}}+{{x}^{2}}-2\) có phương trình \({{x}^{4}}+{{x}^{2}}-2=0\) có hai nghiệm thực nên đồ thị hàm số \(y={{x}^{4}}+{{x}^{2}}-2\) cắt trục hoành.
D. Ta thấy chỉ có hàm số \(y=\frac{1}{4}{{x}^{4}}+{{x}^{2}}+1\) thỏa mãn đầy đủ các yêu cầu trên.
Chọn D.







