Câu hỏi
Cho hàm số \(f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d\)\(\left( a,b,c,d\in \mathbb{R},a\ne 0 \right)\)có bảng biến thiên như hình bên.
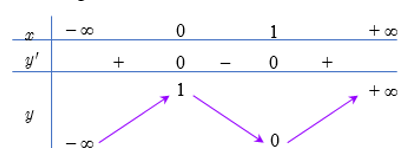
Tìm tất cả các giá trị thực của \(m\) để phương trình \(\left| f(x) \right|=m\) có 4 nghiệm phân biệt thỏa mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}<\frac{1}{2}<{{x}_{4}}\).
- A \(0<m<1\)
- B \(\frac{1}{2}<m<1\)\
- C \(0<m\le 1\)
- D \(\frac{1}{2}\le m<1\)
Phương pháp giải:
+) Từ BBT của hàm số \(y=f\left( x \right)\) ta xác định đực các hệ số \(a,b,c,d\).
+) Vẽ BTT của hàm số \(y=\left| f\left( x \right) \right|\) sau đó dựa vào sự tương giao của \(y=\left| f\left( x \right) \right|\) và \(y=m\) để biện luận số nghiệm theo yêu cầu.
Lời giải chi tiết:
Từ bảng biến thiên ta có : \(f\left( 0 \right)=1\Rightarrow d=1\).
\({f}'\left( x \right)=3a{{x}^{2}}+2bx+c\), \({f}'\left( 0 \right)=0\Rightarrow c=0.\)
\(\left\{ \begin{array}{l}f'\left( 1 \right) = 0\\f\left( 1 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a + 2b + c = 0\\a + b + c + d = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 2\\b = - 3\end{array} \right.\).
Suy ra \(f\left( x \right)=2{{x}^{3}}-3{{x}^{2}}+1\). Từ đó ta có bảng biến thiên của hàm số \(y=\left| f(x) \right|\) như sau
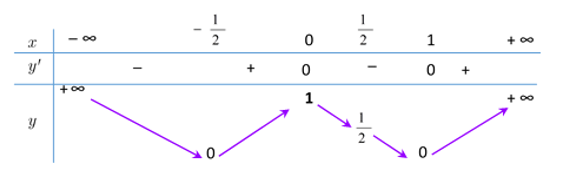
Dựa vào bảng biến thiên, ta thấy để phương trình \(\left| f(x) \right|=m\) có 4 nghiệm phân biệt thỏa mãn \({{x}_{1}}<{{x}_{2}}<{{x}_{3}}<\frac{1}{2}<{{x}_{4}}\) thì \(\frac{1}{2}<m<1\).
Chọn B.







