Câu hỏi
Cho một khối tứ diện có thể tích \(V\). Gọi \({V}'\) là thể tích khối đa diện có các đỉnh là trung điểm các cạnh của khối tứ diện đã cho. Tính tỉ số \(\frac{{{V}'}}{V}\)
- A \(\frac{{{V}'}}{V}=\frac{2}{3}\)
- B \(\frac{{{V}'}}{V}=\frac{1}{4}\)
- C \(\frac{{{V}'}}{V}=\frac{5}{8}\)
- D \(\frac{{{V}'}}{V}=\frac{1}{2}\)
Phương pháp giải:
Sử dụng phân chia đa diện và tỉ lệ thể tích \(\frac{{{V}_{S.{A}'{B}'{C}'}}}{{{V}_{S.ABC}}}=\frac{S{A}'}{SA}.\frac{S{B}'}{SB}.\frac{S{C}'}{SC}\) với \({A}'\in SA,{B}'\in SB,{C}'\in SC\).
Lời giải chi tiết:
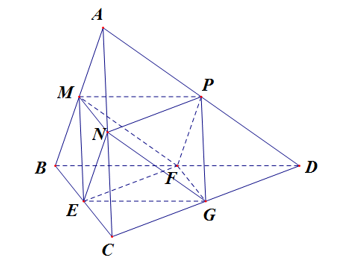
Ta có :
\({V}'=V-\left( {{V}_{A.MNP}}+{{V}_{B.MEF}}+{{V}_{C.NEG}}+{{V}_{D.PFG}} \right)=V-4{{V}_{A.MNP}}=V-4.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.V=\frac{1}{2}V\).
Vậy \(\frac{{{V}'}}{V}=\frac{1}{2}\)
Chọn D.
Câu hỏi trước
