Phương pháp giải:

+) Từ giả thiết \(A{B}'\bot B{C}'\) ta suy ra \(A{B}'\bot BM\) với M là trung điểm của \({A}'{B}'\).

+) Gọi \(A{B}'\bot BM\) tại I. Đặt \(B{B}'=x\) rồi từ tỉ lệ các cạnh và hệ thức lượng ta tính được \(x\).

+) Thể tích lăng trụ \(V=B{B}'.{{S}_{{A}'{B}'{C}'}}\).

Lời giải chi tiết:

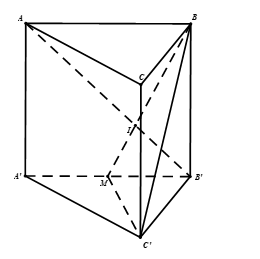
Gọi M là trung điểm của \({A}'{B}'\). Ta có \(\left. \begin{array}{l}C'M \bot AB'\\BC' \bot AB'\end{array} \right\} \Rightarrow AB' \bot BM\) hay \(A{B}'\bot BM\) tại \(I\)

Đặt \(B{B}'=x\) suy ra \(A{B}'=\sqrt{{{a}^{2}}+{{x}^{2}}}\)

Ta có \(\frac{M{B}'}{AB}=\frac{I{B}'}{IA}\) \(\Rightarrow AI=\frac{2}{3}A{B}'=\frac{2}{3}\sqrt{{{a}^{2}}+{{x}^{2}}}\)

Xét tam giác \(AB{B}'\) có \(A{{B}^{2}}=AI.A{B}'\)\(\Leftrightarrow {{a}^{2}}=\frac{2}{3}\left( {{a}^{2}}+{{x}^{2}} \right)\)\(\Leftrightarrow {{x}^{2}}=\frac{{{a}^{2}}}{2}\)\(\Leftrightarrow x=\frac{a\sqrt{2}}{2}\)

Vậy \(V=A{A}'.{{S}_{\Delta ABC}}=\frac{a\sqrt{2}}{2}.\frac{{{a}^{2}}\sqrt{3}}{4}=\frac{{{a}^{3}}\sqrt{6}}{8}\)

Chọn C.